题目内容
9.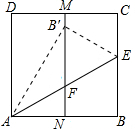 如图,正方形ABCD中,M,N分别是DC、AB的中点,沿过点A的直线折叠,使点B落在MN上,落点为B′,折痕交BC于点E,交MN于点F,再把这个正方形展开,若B′F=3cm,则AB=3$\sqrt{3}$cm.
如图,正方形ABCD中,M,N分别是DC、AB的中点,沿过点A的直线折叠,使点B落在MN上,落点为B′,折痕交BC于点E,交MN于点F,再把这个正方形展开,若B′F=3cm,则AB=3$\sqrt{3}$cm.
分析 根据折叠的性质得到AB′=AB,在Rt△BNF中,根据三角函数的定义得到sin∠AB′N=$\frac{AN}{AB′}$=$\frac{1}{2}$,求得∠BNF=30°,根据平行线的性质得到∠DAB′=30°,∠B′AN=60°,根据直角三角形的性质得到FN=$\frac{1}{2}$AF,设FN=x,则AN=$\sqrt{3}$x,AF=B′F=2x=3,解直角三角形得到AN=$\frac{3\sqrt{3}}{2}$,于是得到结论.
解答 解:∵△AB′E是由△ABE翻折得到的,
∴AB′=AB,又点N为AB的中点,
在Rt△BNF中,sin∠AB′N=$\frac{AN}{AB′}$=$\frac{1}{2}$,
∴∠BNF=30°,
∵MN∥AD,
∴∠DAB′=30°,∠B′AN=60°,
∴∠B′AE=∠BAE=30°,
∴∠AB′F=∠B′AF,
∴AF=B′F,
∴FN=$\frac{1}{2}$AF,
设FN=x,则AN=$\sqrt{3}$x,AF=B′F=2x=3,
解得:x=$\frac{3}{2}$,
∴AN=$\frac{3\sqrt{3}}{2}$,
∴AB=2AN=3$\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 本题考查了翻折变换的性质,全等三角形的性质,正方形的性质,勾股定理,熟记性质是解题的关键,难点在于利用勾股定理列出方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.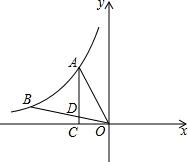 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )| A. | 1 | B. | -$\frac{8}{3}$ | C. | -$\frac{9}{8}$ | D. | -$\frac{9}{4}$ |
18.在平面直角坐标系中,点(-1,2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.函数y=$\frac{k}{x}$的图象经过点(2,3),则k=( )
| A. | 2 | B. | 3 | C. | 6 | D. | -6 |
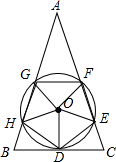 如图,五边形DEFGH是边长为2的正五边形,⊙O是正五边形DEFGH的外接圆,过点D作⊙D的切线,与GH、FE的延长线交分别于点B和C,延长HG、EF相交于点A,那么AB的长度是2+2$\sqrt{5}$.
如图,五边形DEFGH是边长为2的正五边形,⊙O是正五边形DEFGH的外接圆,过点D作⊙D的切线,与GH、FE的延长线交分别于点B和C,延长HG、EF相交于点A,那么AB的长度是2+2$\sqrt{5}$.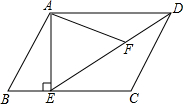 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.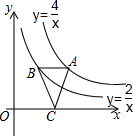 如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,过点A作AB∥x轴,交函数y=$\frac{2}{x}$(x>0)的图象于点B,点C在x轴上,连接AC、BC.则△ABC的面积是1.
如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,过点A作AB∥x轴,交函数y=$\frac{2}{x}$(x>0)的图象于点B,点C在x轴上,连接AC、BC.则△ABC的面积是1.
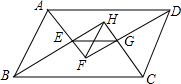 如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD与∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.求证:EG=FH.
如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD与∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.求证:EG=FH.