题目内容
13.已知一次函数y=kx+b的图象经过点(2,0),(1,3),则不求k,b的值,可直接得到方程kx+b=3的解是x=1.分析 利用一次函数图象上点的坐标特征可判断x=1时,y=3,然后利用一次函数与一元一次方程的关系可得到方程kx+b=3的解.
解答 解:∵一次函数y=kx+b的图象经过点(1,3),
∴当x=1时,y=3,即kx+b=3,
即方程kx+b=3的解是x=1.
点评 本题考查了一次函数与一元一次方程的关系:任何一元一次方程都可以转化为ax+b=0 (a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值.从图象上看,相当于已知直线y=ax+b确定它与x轴的交点的横坐标的值.

练习册系列答案
相关题目
4.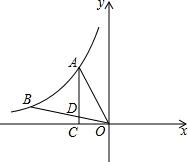 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )| A. | 1 | B. | -$\frac{8}{3}$ | C. | -$\frac{9}{8}$ | D. | -$\frac{9}{4}$ |
18.在平面直角坐标系中,点(-1,2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
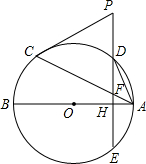 如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.
如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.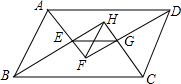 如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD与∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.求证:EG=FH.
如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD与∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.求证:EG=FH.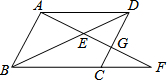 如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=$\frac{16}{3}$.
如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=$\frac{16}{3}$. 如图.抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线上位于直线AB上方的一点(不与点A,B重合),连接AD,BD.
如图.抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线上位于直线AB上方的一点(不与点A,B重合),连接AD,BD.