题目内容
3.若m1,m2…m2017是从0,1,2这三个数中取值的一列数.若m1+m2+…+m2017=1527.(m1-1)2+(m2-1)2+…+(m2017-1)2=1510,则在m1,m2…m2017中取值为2的个数为510.分析 通过m1,m2,…m2017是从0,1,2这三个数中取值的一列数,(m1-1)2+(m2-1)2+…+(m2017-1)2=1510从而得到1的个数,由m1+m2+…+m2017=1527得到2的个数.
解答 解:∵(m1-1)2+(m2-1)2+…+(m2017-1)2=1510,
∵m1,m2,…,m2017是从0,1,2这三个数中取值的一列数,
∴m1,m2,…,m2017中为1的个数是2017-1510=507,
∵m1+m2+…+m2017=1527,
∴2的个数为(1527-507)÷2=510个,
故答案为:510.
点评 此题考查数字的变化规律和完全平方的性质,找出运算的规律.利用规律解决问题.

练习册系列答案
相关题目
13.抛物线y=(x-1)2+t与x轴的两个交点之间的距离为4,则t的值是( )
| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
14. 如图,在平面直角坐标系中,点A是反比例函数y=$\frac{m}{x}$的图象上的一点,过点A作AB⊥x轴于点B,点C在y轴的负半轴上,连接AC,BC.若△ABC的面积为5,则m的值为( )
如图,在平面直角坐标系中,点A是反比例函数y=$\frac{m}{x}$的图象上的一点,过点A作AB⊥x轴于点B,点C在y轴的负半轴上,连接AC,BC.若△ABC的面积为5,则m的值为( )
 如图,在平面直角坐标系中,点A是反比例函数y=$\frac{m}{x}$的图象上的一点,过点A作AB⊥x轴于点B,点C在y轴的负半轴上,连接AC,BC.若△ABC的面积为5,则m的值为( )
如图,在平面直角坐标系中,点A是反比例函数y=$\frac{m}{x}$的图象上的一点,过点A作AB⊥x轴于点B,点C在y轴的负半轴上,连接AC,BC.若△ABC的面积为5,则m的值为( )| A. | -10 | B. | 10 | C. | -5 | D. | 5 |
11.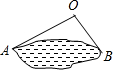 如图所示,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
如图所示,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
 如图所示,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
如图所示,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )| A. | 5米 | B. | 15米 | C. | 10米 | D. | 20米 |
 如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AF.连结DC、BE交于F点.
如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AF.连结DC、BE交于F点.