题目内容
8. 如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AF.连结DC、BE交于F点.
如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AF.连结DC、BE交于F点.(1)求证:△DAC≌△BAE.
(2)直线DC、BE是否互相垂直,请说明理由.
(3)求证:AF平分∠DFE.
分析 (1)由题意可得AD=AB,AC=AE,由∠DAB=∠CAE=90°,可得到∠DAC=∠BAE,从而可证△DAC≌△BAE;
(2)由(1)可得∠ACD=∠AEB,再利用直角三角形的性质及等量代换即可得到结论;
(3)作AM⊥DC于M,AN⊥BE于N,利用全等三角形的面积相等及角平分线的判定即可证得结论.
解答 解:
(1)∵∠DAB=∠CAE=90°,
∴∠DAB+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,
又∵AD=AB,AC=AE,
在△DAC与△BAE中
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$
∴△DAC≌△BAE;
(2)DC⊥BE.
理由是:
∵△DAC≌△BAE
∴∠ACD=∠AEB
∵∠AEB+∠ANE=90°
∠ANE=∠FNC
∴∠FNC+∠ACD=90°
∴∠NFC=90°
∴DC⊥BE
(3)如图,作AM⊥DC于M,AN⊥BE于N,
∵△DAC≌△BAE
∴S△DAC=S△BAE,DC=BE,
∴$\frac{1}{2}$DC•AM=$\frac{1}{2}$BE•AN,
∴AM=AN,
∴AF平分∠DFE.
点评 本题主要考查全等三角形的判定和性质,及直角三角形的性质,角平分线的判定,熟练掌握全等三角形的判定和性质是解决本题的关键.

练习册系列答案
相关题目
18.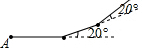 如图所示,小华从A点出发,沿直线前进10米后左转20°,再沿直线前进10米,又向左转20°,…照这样走下去,他第一次回到出发地A时,一共走的路程是( )
如图所示,小华从A点出发,沿直线前进10米后左转20°,再沿直线前进10米,又向左转20°,…照这样走下去,他第一次回到出发地A时,一共走的路程是( )
 如图所示,小华从A点出发,沿直线前进10米后左转20°,再沿直线前进10米,又向左转20°,…照这样走下去,他第一次回到出发地A时,一共走的路程是( )
如图所示,小华从A点出发,沿直线前进10米后左转20°,再沿直线前进10米,又向左转20°,…照这样走下去,他第一次回到出发地A时,一共走的路程是( )| A. | 140米 | B. | 150米 | C. | 160米 | D. | 180米 |
19. 如图,已知AB=A1B,A1B1=A1B2,A2B2=A2B3,A3B3=A3B4,…若∠A=70°,则∠An的度数为( )
如图,已知AB=A1B,A1B1=A1B2,A2B2=A2B3,A3B3=A3B4,…若∠A=70°,则∠An的度数为( )
 如图,已知AB=A1B,A1B1=A1B2,A2B2=A2B3,A3B3=A3B4,…若∠A=70°,则∠An的度数为( )
如图,已知AB=A1B,A1B1=A1B2,A2B2=A2B3,A3B3=A3B4,…若∠A=70°,则∠An的度数为( )| A. | $\frac{70}{{2}^{n}}$ | B. | $\frac{70}{{2}^{n+1}}$ | C. | $\frac{70}{{2}^{n-1}}$ | D. | $\frac{70}{{2}^{n+2}}$ |
16.如(x+a)与(x+3)的乘积中不含x的一次项,则a的值为( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
 如图所示:
如图所示: 如图,一个花坛由两个半圆和一个长方形组成,已知长方形的长为a米,宽为b米.
如图,一个花坛由两个半圆和一个长方形组成,已知长方形的长为a米,宽为b米.