��Ŀ����
18������������ֱ�������֣�-1��1��2�Ŀ�Ƭ�����dz����ֲ�ͬ������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ���г��һ�ż������֣��Ż�ϴ�Ⱥ��ٴ���������һ�ż������֣���1�������б�������ͼ�ķ�����ֻѡ����һ�֣�����ʾ���γ����Ƭ�ϵ����ֵ����н����
��2������һ�γ����������Ϊ��ĺ�����x���ڶ��γ����������Ϊ���������y����㣨x��y������˫����y=$\frac{2}{x}$�ϵĸ��ʣ�
���� ��1��������״ͼ���ɵý⣻
��2�����ݷ���������ͼ���ϵ�����������жϳ���˫����y=$\frac{2}{x}$�ϵ���������ٸ��ݸ��ʹ�ʽ��ʽ���㼴�ɵý⣮
��� �⣺��1���������⻭����״ͼ���£�
��2����x=-1ʱ��y=$\frac{2}{-1}$=-2����x=1ʱ��y=$\frac{2}{1}$=2����x=2ʱ��y=$\frac{2}{2}$=1��
��һ����9�ֵȿ��ܵ�������㣨x��y������˫����y=$\frac{2}{x}$����2���������1��2������2��1����
��㣨x��y������˫����y=$\frac{2}{x}$�ϵĸ���Ϊ��$\frac{2}{9}$��
���� ���⿼�����б�������״ͼ���Լ�����������ͼ���ϵ���������������ݳ鿨�Ĺ�������״ͼ��ʾ���γ����Ƭ�ϵ����ֵ����н���ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
8������ͼ���У���һ�������IJ���չ��ͼ��������
| A�� |  | B�� |  | C�� |  | D�� |  |
9����ͼ�е�ƽ��չ��ͼ���ע������ͼ�β�������ǣ�������
| A�� |  ������ | B�� |  ������ | C�� |  Բ���� | D�� |  ���� |
6��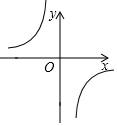 ��֪����y=$\frac{m}{x}$��ͼ����ͼ�����½��ۣ�
��֪����y=$\frac{m}{x}$��ͼ����ͼ�����½��ۣ�
��m��0��
����ÿ����֧��y��x�����������
������A��-1��a������B��2��b����ͼ���ϣ���a��b��
������P��x��y����ͼ���ϣ����P1��-x��-y��Ҳ��ͼ���ϣ�������ȷ�ĸ����ǣ�������
 ��֪����y=$\frac{m}{x}$��ͼ����ͼ�����½��ۣ�
��֪����y=$\frac{m}{x}$��ͼ����ͼ�����½��ۣ���m��0��
����ÿ����֧��y��x�����������
������A��-1��a������B��2��b����ͼ���ϣ���a��b��
������P��x��y����ͼ���ϣ����P1��-x��-y��Ҳ��ͼ���ϣ�������ȷ�ĸ����ǣ�������
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
13��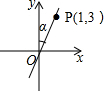 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��OP���㣨1��3������tan����ֵ�ǣ�������
��ͼ����ƽ��ֱ������ϵ�У�ֱ��OP���㣨1��3������tan����ֵ�ǣ�������
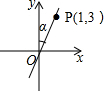 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��OP���㣨1��3������tan����ֵ�ǣ�������
��ͼ����ƽ��ֱ������ϵ�У�ֱ��OP���㣨1��3������tan����ֵ�ǣ�������| A�� | $\frac{1}{3}$ | B�� | 3 | C�� | $\frac{\sqrt{10}}{10}$ | D�� | $\frac{3\sqrt{10}}{10}$ |
9����֪a2b=-1����-ab��a3b-a����ֵ���ڣ�������
| A�� | -2 | B�� | 0 | C�� | 1 | D�� | 2 |
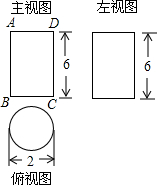 һ�������������ͼ��ͼ��ʾ�����һֻ����Ҫ������������еĵ�B�������ر�������CD���е�E��������������·�����·����
һ�������������ͼ��ͼ��ʾ�����һֻ����Ҫ������������еĵ�B�������ر�������CD���е�E��������������·�����·����