题目内容
13.抛物线y=(x-1)2+t与x轴的两个交点之间的距离为4,则t的值是( )| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
分析 利用求根公式易得方程的两根,让两根之差的绝对值为4列式求值即可.
解答 解:设抛物线y=(x-1)2+t与x轴的两个交点为(x1,0),(x2,0),
则x1=1-$\sqrt{-t}$,x2=1+$\sqrt{-t}$,
∴|x1-x2|=4,
∴(1+$\sqrt{-t}$)-(1-$\sqrt{-t}$)=4,
∴t=-4.
故选D.
点评 本题考查了抛物线与x轴的交点,二次函数与一元二次方程的关系,利用求根公式列出关于t的方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列图形中,哪一个是棱锥的侧面展开图( )
| A. |  | B. |  | C. |  | D. |  |
18.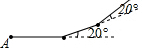 如图所示,小华从A点出发,沿直线前进10米后左转20°,再沿直线前进10米,又向左转20°,…照这样走下去,他第一次回到出发地A时,一共走的路程是( )
如图所示,小华从A点出发,沿直线前进10米后左转20°,再沿直线前进10米,又向左转20°,…照这样走下去,他第一次回到出发地A时,一共走的路程是( )
 如图所示,小华从A点出发,沿直线前进10米后左转20°,再沿直线前进10米,又向左转20°,…照这样走下去,他第一次回到出发地A时,一共走的路程是( )
如图所示,小华从A点出发,沿直线前进10米后左转20°,再沿直线前进10米,又向左转20°,…照这样走下去,他第一次回到出发地A时,一共走的路程是( )| A. | 140米 | B. | 150米 | C. | 160米 | D. | 180米 |
5. 如图,等边△ABO的顶点O与原点重合,点A的坐标是(-4,0),点B在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是( )
如图,等边△ABO的顶点O与原点重合,点A的坐标是(-4,0),点B在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是( )
 如图,等边△ABO的顶点O与原点重合,点A的坐标是(-4,0),点B在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是( )
如图,等边△ABO的顶点O与原点重合,点A的坐标是(-4,0),点B在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是( )| A. | 2$\sqrt{3}$ | B. | -2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | -4$\sqrt{3}$ |

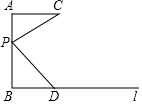 如图,线段AC和直线l分别垂直线段AB于点A,B.点P是线段AB上的一个动点,由A移动到B,连接CP,过点P作PD⊥CP交l于点D,设线段AP的长为x,BD的长为y,在下列图象中,能大致表示y与x之间函数关系的是( )
如图,线段AC和直线l分别垂直线段AB于点A,B.点P是线段AB上的一个动点,由A移动到B,连接CP,过点P作PD⊥CP交l于点D,设线段AP的长为x,BD的长为y,在下列图象中,能大致表示y与x之间函数关系的是( )