题目内容
20.已知a,b,c都是有理数,且满足$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1,求6-$\frac{abc}{|abc|}$的值.分析 首先依据足$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1,可确定出a、b、c中负数的个数,然后可确定出$\frac{abc}{|abc|}$的值,最后进行计算即可.
解答 解:∵$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1,
∴a、b、c中有1个负数,
∴$\frac{abc}{|abc|}$=-1.
∴6-$\frac{abc}{|abc|}$的=6-(-1)=6+1=7.
点评 本题主要考查的是绝对值的性质,求得a、b、c中负数的个数是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
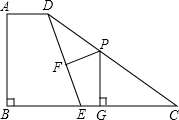 已知,如图,在四边形ABCD中,AD∥BC,∠B=90°,点E在BC上,∠CDE=∠C,点P在CD上,PF⊥DE、PG⊥BC,点F、G为垂足,求证.PF+PG=AB.
已知,如图,在四边形ABCD中,AD∥BC,∠B=90°,点E在BC上,∠CDE=∠C,点P在CD上,PF⊥DE、PG⊥BC,点F、G为垂足,求证.PF+PG=AB.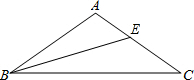 如图,△ABC中,∠A=100°,AB=AC,BE是△ABC的平分线.求证:AE+BE=BC.
如图,△ABC中,∠A=100°,AB=AC,BE是△ABC的平分线.求证:AE+BE=BC.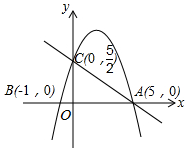 如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(-1,0)两点,与y轴交于点C(0,$\frac{5}{2}$).
如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(-1,0)两点,与y轴交于点C(0,$\frac{5}{2}$).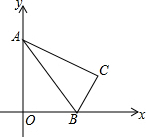 如图,在平面直角坐标系中,点A的坐标为(0,$\sqrt{3}$),点B的坐标为(1,0),将△AOB沿直线AB折叠,点O在点C处,则点C的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
如图,在平面直角坐标系中,点A的坐标为(0,$\sqrt{3}$),点B的坐标为(1,0),将△AOB沿直线AB折叠,点O在点C处,则点C的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).