Question

9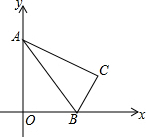．如图，在平面直角坐标系中，点A的坐标为（0，$\sqrt{3}$），点B的坐标为（1，0），将△AOB沿直线AB折叠，点O在点C处，则点C的坐标为（$\frac{3}{2}$，$\frac{\sqrt{3}}{2}$）．

Answer 1

分析 作CD⊥x轴于D，根据坐标与图形特征求出OA、OB，根据翻转变换的性质求出BC和∠CBD，根据正弦和余弦的定义分别求出BD、CD，计算即可．

解答 解：作CD⊥x轴于D，
由题意得，OB=1，OA=$\sqrt{3}$，
∴tan∠OAB=$\frac{OB}{OA}$=$\frac{\sqrt{3}}{3}$，
∴∠OAB=30°，
∴∠OBA=60°，
由翻转变换的性质可知，BC=OB=1，∠CBD=180°-60°×2=60°，
∴BD=BC×cos∠CBD=$\frac{1}{2}$，CD=BC×sin∠CBD=$\frac{\sqrt{3}}{2}$，
∴点C的坐标为：（$\frac{3}{2}$，$\frac{\sqrt{3}}{2}$），
故答案为：（$\frac{3}{2}$，$\frac{\sqrt{3}}{2}$）．

点评 本题考查的是翻转变换的性质、坐标与图形变化，掌握翻转变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解题的关键．