题目内容
5.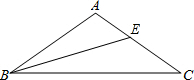 如图,△ABC中,∠A=100°,AB=AC,BE是△ABC的平分线.求证:AE+BE=BC.
如图,△ABC中,∠A=100°,AB=AC,BE是△ABC的平分线.求证:AE+BE=BC.
分析 延长BE到F,使BF=BC,连接FC,由AB=AC,∠A=100°,得到∠ABC=∠ACB=40°,由于BE平分∠ABC,于是得到∠ABE=∠EBC=20°,通过△FCE≌△F′CE,得到EF=EF′,∠EF′C=∠F=80°,证得△ABE≌△F′BE,于是得到AE=EF′,于是得到结论.
解答 解:如图,延长BE到F,使BF=BC,连接FC,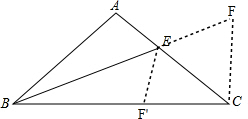 ∵AB=AC,∠A=100°,
∵AB=AC,∠A=100°,
∴∠ABC=∠ACB=40°,
∵BE平分∠ABC,
∴∠ABE=∠EBC=20°,
∵BF=BC,
∴∠F=∠BCF=80°,
∴∠FCE=∠ACB=40°,
在BC上取CF′=CF,连接EF′,
在△FCE与△F′CE中,$\left\{\begin{array}{l}{CF=CF′}&{\;}\\{∠F′CE=∠FCE}&{\;}\\{CE=CE}&{\;}\end{array}\right.$,
∴△FCE≌△F′CE(SAS),
∴EF=EF′,∠EF′C=∠F=80°,
∴∠BF′E=100°,
∴∠A=∠BF′E,
在△ABE与△BF′E中,$\left\{\begin{array}{l}{∠A=∠BF′E}&{\;}\\{∠ABE=∠F′BE}&{\;}\\{BE=BE}&{\;}\end{array}\right.$,
∴△ABE≌△F′BE(AAS),
∴AE=EF′,
∴AE=EF,
∴AE+BE=BE+EF=BC.
点评 本题考查了全等三角形的判定和性质,角平分线的性质,等腰三角形的性质,作辅助线构建全等三角形是解题的关键.

练习册系列答案
相关题目
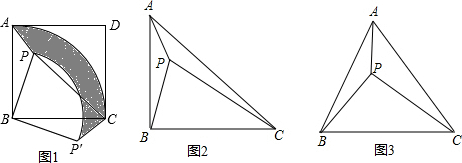
 如图,点D、E、F、B在同一直线上,∠B=∠D.DE=BF,要使△ABE≌△CDF(不再添加新的线段和字母),需添加的一个条件是AB=CD(只写一个条件即可)
如图,点D、E、F、B在同一直线上,∠B=∠D.DE=BF,要使△ABE≌△CDF(不再添加新的线段和字母),需添加的一个条件是AB=CD(只写一个条件即可)