题目内容
18.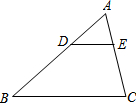 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )| A. | 3:2 | B. | 3:5 | C. | 2:5 | D. | 2:3 |
分析 由DE∥BC可得△ADE∽△ABC,根据相似三角形性质可得.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{2}{5}$,
∴$\frac{AD}{DB}$=$\frac{2}{3}$,
故选:D.
点评 本题主要考查相似三角形的判定与性质,平行于三角形一边的直线和其它两边(或两边的延长线)相交,所截得的三角形与原三角形相似.

练习册系列答案
相关题目
9.下列方程中,属于一元二次方程的是( )
| A. | $\frac{1}{{x}^{2}}+\frac{1}{x}-3=0$ | B. | ax2+bx+c=0 | C. | x2+5x=x2-3 | D. | x2-3x+2=0 |
6.已知空气的单位体积质量为1,29×10-3克/厘米3,1.29×10-3用小数表示为( )
| A. | 0.00129 | B. | 0.0129 | C. | -0.00129 | D. | 0.000129 |
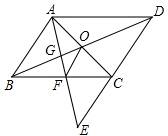 如图,在?ABCD中,F是边BC的中点,连接AF交DC的延长线于点E,AC,BD相交于点O,AF交BD于点G,连接OF,判断EC与OF的位置关系和大小关系,并证明你的结论.
如图,在?ABCD中,F是边BC的中点,连接AF交DC的延长线于点E,AC,BD相交于点O,AF交BD于点G,连接OF,判断EC与OF的位置关系和大小关系,并证明你的结论.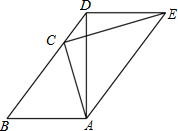 如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE.
如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE. 如图,矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),反比例函数y=$\frac{k}{x}(k≠0)$在第一象限内的图象过矩形OABC的对角线的交点M,并与AB、BC分别交于点E、F,连接OE、EF、OF,则△OEF的面积为$\frac{75}{4}$.
如图,矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),反比例函数y=$\frac{k}{x}(k≠0)$在第一象限内的图象过矩形OABC的对角线的交点M,并与AB、BC分别交于点E、F,连接OE、EF、OF,则△OEF的面积为$\frac{75}{4}$.