题目内容
两个同心圆,小圆半径2cm,大圆半径4cm,点Q在圆环内无规则自由运动,如果在某一时刻突然停下来,那么点Q与点O距离小于3cm的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概率
专题:
分析:点P与点O的距离小于3cm,也就是说以O点为圆心,3CM为半径作一个圆,这个圆的面积减去小圆的面积就是点P与点O的距离小于3cm的机会(一个圆环的面积),而P可能落在的面积为大圆面积减小圆面积,也就是整个圆环的面积,点Q与点O距离小于3cm的概率=小圆环的面积:大圆环的面积.
解答:解:如图所示,

S大圆环=42π-22π=12π,
S小圆环=32π-22π=5π,
所以,点Q与点O距离小于3cm的概率=
=
.
故选A.

S大圆环=42π-22π=12π,
S小圆环=32π-22π=5π,
所以,点Q与点O距离小于3cm的概率=
| 5π |
| 12π |
| 5 |
| 12 |
故选A.
点评:此题考查了几何概率的计算公式,用到的知识点为:概率=相应的面积与总面积之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,AB=AC,那么在这个三角形中,三线重合的线段是( )
| A、∠A的平分线,AB边上的中线,AB边上的高 |
| B、∠A的平分线,BC边上的中线,BC边上的高 |
| C、∠B的平分线,AC边上的中线,AC边上的高 |
| D、∠C的平分线,AB边上的中线,AB边上的高 |
下列命题:(1)一组邻边相等的平行四边形是菱形;(2)一组邻边相等的矩形是正方形;(3)一组对边平行且相等的四边形是平行四边形;(4)一组对边相等且有一个角是直角的四边形是矩形.其中真命题的个数为( )
| A、0个 | B、1个 | C、2个 | D、3个 |
以下列各组数为边的三角形不是直角三角形的是( )
| A、5,6,9 |
| B、5,3,4 |
| C、24,10,26 |
| D、60,11,61 |
在半径为10的⊙O中,弦AB=12,弦CD=16,且AB∥CD,则弦AB、CD的距离为( )
| A、14 | B、2 |
| C、8或6 | D、14或2 |
 如图,在平面直角坐标系中,一颗,棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…,如此下去.则经过第2013次跳动之后,棋子落点的坐标为
如图,在平面直角坐标系中,一颗,棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…,如此下去.则经过第2013次跳动之后,棋子落点的坐标为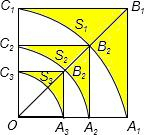 如图,正方形OA1B1C1的边长为2,以O为圆心,OA1为半径作弧A1C1交OB1于点B2,设弧A1C1与边A1B1,B1C1围成的阴影部分的面积为S1.然后以OB2为对角线作正方形OA2B2C2,又以O为圆心、OA2为半径作弧A2C2交OB2于点B3,设弧A2C2与边A2B2、B2C2围成的阴影部分的面积为S2,…,按此规律继续作下去,设弧AnCn,BnCn围成的阴影部分的面积为Sn,设S=S1+S2+S2+…+Sn,则S=
如图,正方形OA1B1C1的边长为2,以O为圆心,OA1为半径作弧A1C1交OB1于点B2,设弧A1C1与边A1B1,B1C1围成的阴影部分的面积为S1.然后以OB2为对角线作正方形OA2B2C2,又以O为圆心、OA2为半径作弧A2C2交OB2于点B3,设弧A2C2与边A2B2、B2C2围成的阴影部分的面积为S2,…,按此规律继续作下去,设弧AnCn,BnCn围成的阴影部分的面积为Sn,设S=S1+S2+S2+…+Sn,则S=