题目内容
14．已知一次函数y=（1-a）x+4a-1的图象．（1）经过原点，求a；
（2）与直线y=2x平行，求a．
分析 （1）根据直线过原点可知当x=0时，y=0，由此可得出a的值，再根据一次函数的定义得出a的取值范围，进而可得出结论；
（2）根据平行线的性质即可得出结论．
解答 解：（1）∵一次函数y=（1-a）x+4a-1的图象经过原点，
∴4a-1=0，解得a=$\frac{1}{4}$，
∵当x=$\frac{1}{4}$时，1-a≠0，
∴a=$\frac{1}{4}$符合题意；
（2）∵与直线y=2x平行，
∴1-a=2，解得a=-1．
点评 本题考查的是一次函数图象上点的坐标特征，熟知一次函数图象上图象上点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
一架云梯长10m，如图所示斜靠在一面墙上，梯子底端C离墙6m．
2．
如图，将Rt△ABC，其中∠B=30°，∠C=90°，AC=1，绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，那么，点B所运动的路径长（ ）
如图，将Rt△ABC，其中∠B=30°，∠C=90°，AC=1，绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，那么，点B所运动的路径长（ ）| A． | 2$\sqrt{3}$ | B． | 4 | C． | $\frac{4π}{3}$ | D． | $\frac{2\sqrt{3}π}{3}$ |
如图是一数值转换机，若输出的结果为-48，则输入的x的值为±4．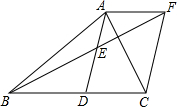
如图，在△ABC中，AD是BC边的中线，E是AD的中点，过A点作AF∥BC交BE的延长线于点F，连结CF．求证：四边形ADCF是平行四边形．