题目内容
5.某工艺品每件的成本是50元,在某段时间内若以每件x元出售,可卖出(200-2x)件,设这殷肘间内售出该工艺品的利润为y元.(1)直接接写出利润y(元)与售价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果要使利润不低于1200元,且成本不超过2500元,请直接写出x的取值范围为75≤x≤80.
分析 (1)利用销量×每件利润进而得出y与x的函数关系式;
(2)利用配方法求二次函数最值方法得出即可;
(3)根据题意列不等式组即可得到结果.
解答 解:(1)由题意可得:y=(x-50)(200-2x)=-2x2+300x-10000;
(2)由题意可得:
y=-2x2+300x-10000
=-2(x-75)2+1225,
当x=75时,函数有最大值1250,
答:当定价为75元/件时,每天的销售利润最大,最大利润是1250元;
(3)根据题意得:$\left\{\begin{array}{l}{-2{x}^{2}+300x-10000≥1200}\\{50(200-2x)≤2500}\end{array}\right.$,
解得:75≤x≤80,
故x的取值范围为75≤x≤80.
故答案为:75≤x≤80.
点评 此题主要考查了二次函数的应用以及一元二次方程的应用,正确得出y与x的函数关系式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,已知∠ABC=30°,∠CBD=80°,BE是∠ABD的平分线,求∠CBE的度数.
如图所示,已知∠ABC=30°,∠CBD=80°,BE是∠ABD的平分线,求∠CBE的度数. 如图.在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的与反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于二、四象限A(-4,3),B(6,n)的点.
如图.在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的与反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于二、四象限A(-4,3),B(6,n)的点.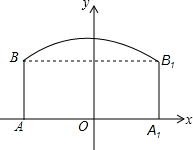 如图,隧道的截面由抛物线和长方形构成,长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.
如图,隧道的截面由抛物线和长方形构成,长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m. 如图,直线l1∥l2,AC=10,DE=3,EF=2,则AB的长是6.
如图,直线l1∥l2,AC=10,DE=3,EF=2,则AB的长是6.