题目内容
4. 一架云梯长10m,如图所示斜靠在一面墙上,梯子底端C离墙6m.
一架云梯长10m,如图所示斜靠在一面墙上,梯子底端C离墙6m.(1)这个梯子的顶端A距地面有多高?
(2)如果梯子的顶端下滑了2m,那么梯子的底部在水平方向也是滑动了2m吗?
分析 (1)直接根据勾股定理求出AB的长即可;
(2)先根据梯子的顶端下滑了2米求出AD的长,再根据勾股定理求出BE的长,进而可得出结论.
解答 解:(1)由题意可知△ABC是直角三角形
∵BC=6m AC=10m
∴由勾股定理得:
AB=$\sqrt{1{0}^{2}-{6}^{2}}$=8(m),
∴梯子的高为8米;
(2)由题意可知AC=DE=10m,
∵AD=2m,
∴BD=8-2=6(m),
在Rt△DBE中,由勾股定理得:
BE=$\sqrt{D{E}^{2}-B{D}^{2}}$
=8(m),
∴CE=BE-BC=8-6=2(m),
即CE=AD,
答:梯子的底部在水平方向也是滑动了2m.
点评 此题主要考查了勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
14.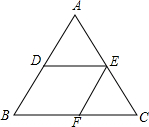 如图,DE∥BC,EF∥AC,则下列比例式中不正确的是( )
如图,DE∥BC,EF∥AC,则下列比例式中不正确的是( )
 如图,DE∥BC,EF∥AC,则下列比例式中不正确的是( )
如图,DE∥BC,EF∥AC,则下列比例式中不正确的是( )| A. | $\frac{AE}{AC}=\frac{AD}{AB}$ | B. | $\frac{AE}{EC}=\frac{BF}{FC}$ | C. | $\frac{AD}{BD}=\frac{BF}{FC}$ | D. | $\frac{BD}{AD}=\frac{BF}{FC}$ |
9.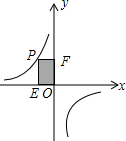 如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为5.这个函数的解析式为( )
如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为5.这个函数的解析式为( )
 如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为5.这个函数的解析式为( )
如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为5.这个函数的解析式为( )| A. | y=$\frac{5}{x}$ | B. | y=-$\frac{5}{x}$ | C. | y=$\frac{10}{x}$ | D. | y=-$\frac{x}{5}$ |
 如图所示,已知∠ABC=30°,∠CBD=80°,BE是∠ABD的平分线,求∠CBE的度数.
如图所示,已知∠ABC=30°,∠CBD=80°,BE是∠ABD的平分线,求∠CBE的度数. 如图.在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的与反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于二、四象限A(-4,3),B(6,n)的点.
如图.在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的与反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于二、四象限A(-4,3),B(6,n)的点.