题目内容
2. 如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )
如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | $\frac{4π}{3}$ | D. | $\frac{2\sqrt{3}π}{3}$ |
分析 根据直角三角形两锐角互余求出∠BAC的度数,根据30°角所对的直角边等于斜边的一半得出AB=2AC=2,然后求出旋转角∠BAB1,再根据弧长公式列式进行计算即可得解.
解答 解:∵∠B=30°,∠C=90°,
∴∠BAC=90°-∠B=90°-30°=60°,AB=2AC=2,
∵△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,
∴旋转角∠BAB1=180°-∠BAC=180°-60°=120°,
∴点B所运动的路径长=$\frac{120π×2}{180}$=$\frac{4}{3}$π.
故选C.
点评 本题考查了旋转的性质,弧长的计算,直角三角形两锐角互余的性质,含30°角的直角三角形的性质,求出旋转角的度数是解题的关键.

练习册系列答案
相关题目
11. 如图是由5个相同的小正方体组成的几何体,其主视图是( )
如图是由5个相同的小正方体组成的几何体,其主视图是( )
 如图是由5个相同的小正方体组成的几何体,其主视图是( )
如图是由5个相同的小正方体组成的几何体,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图.在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的与反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于二、四象限A(-4,3),B(6,n)的点.
如图.在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的与反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于二、四象限A(-4,3),B(6,n)的点.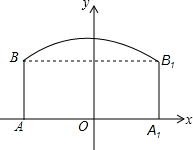 如图,隧道的截面由抛物线和长方形构成,长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.
如图,隧道的截面由抛物线和长方形构成,长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.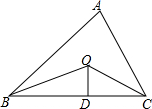 如图,已知△ABC的周长是22,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是多少?
如图,已知△ABC的周长是22,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是多少?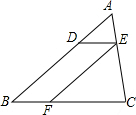 如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )
如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )