题目内容
3.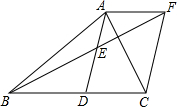 如图,在△ABC中,AD是BC边的中线,E是AD的中点,过A点作AF∥BC交BE的延长线于点F,连结CF.求证:四边形ADCF是平行四边形.
如图,在△ABC中,AD是BC边的中线,E是AD的中点,过A点作AF∥BC交BE的延长线于点F,连结CF.求证:四边形ADCF是平行四边形.
分析 首先利用全等三角形的判定方法得出△AEF≌△DEB(AAS),进而得出AF=BD,再利用一组对边平行且相等的四边形是平行四边形进而得出答案.
解答 证明:∵AF∥BC,∴∠AFE=∠EBD.
在△AEF和△DEB中
∵$\left\{\begin{array}{l}{∠AFE=∠DBE}\\{∠FEA=∠BED}\\{AE=DE}\end{array}\right.$,
∴△AEF≌△DEB(AAS).
∴AF=BD.
∴AF=DC.
又∵AF∥BC,
∴四边形ADCF为平行四边形.
点评 此题主要考查了平行四边形的判定以及全等三角形的判定与性质,得出△AEF≌△DEB是解题关键.

练习册系列答案
相关题目
11. 如图是由5个相同的小正方体组成的几何体,其主视图是( )
如图是由5个相同的小正方体组成的几何体,其主视图是( )
 如图是由5个相同的小正方体组成的几何体,其主视图是( )
如图是由5个相同的小正方体组成的几何体,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
18. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
 如图.在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的与反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于二、四象限A(-4,3),B(6,n)的点.
如图.在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的与反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于二、四象限A(-4,3),B(6,n)的点.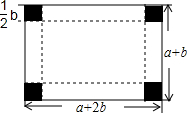 红枣丰收了,为了运输方便,小华的爸爸打算把一个长为(a+2b)cm、宽为(a+b)cm的长方形纸板制成一个有底无盖的盒子,在长方形纸板的四个角各截去一个边长为$\frac{1}{2}$bcm的小正方形,然后沿折线折起即可,如图所示,现将盒子的外表面贴上彩色花板.
红枣丰收了,为了运输方便,小华的爸爸打算把一个长为(a+2b)cm、宽为(a+b)cm的长方形纸板制成一个有底无盖的盒子,在长方形纸板的四个角各截去一个边长为$\frac{1}{2}$bcm的小正方形,然后沿折线折起即可,如图所示,现将盒子的外表面贴上彩色花板. 如图,直线l1∥l2,AC=10,DE=3,EF=2,则AB的长是6.
如图,直线l1∥l2,AC=10,DE=3,EF=2,则AB的长是6.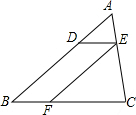 如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )
如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )