题目内容
17.已知m是方程x2-2008x+1=0的一个根,求代数式2m2-4015m-2+$\frac{2008}{{m}^{2}+1}$的值.分析 将一个根m代入x2-2008x+1=0,可得:m2-2008m+1=0,故有m2-2008m=-1,和m2+1=2008m;代入要求的代数式,整理化简即可.
解答 解:根据题意将x=m代入方程x2-2008x+1=0得:m2-2008m+1=0,
即m2-2008m=-1,m2+1=2008m,
∴原式=2(m2-2008m)+m-2+$\frac{2008}{2008m}$
=-2+m-2+$\frac{1}{m}$
=$\frac{{m}^{2}+1}{m}$-4
=$\frac{2008m}{m}$-4
=2008-4
=2004.
点评 本题考查一元二次方程解,能使方程左右两边相等的未知数的值是方程的解,将其代入方程去推理、判断;解题时应注意把m2-2008m、m2+1当成一个整体.利用了整体的思想.

练习册系列答案
相关题目
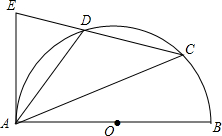 如图,AB是半圆⊙O的直径,点C是半圆上一个动点(不与点A,B重合),点D是弧AC的中点,延长CD交经过点A的切线于点E,连接AD,当△ADE是等腰三角形时,求∠BAC的度数.
如图,AB是半圆⊙O的直径,点C是半圆上一个动点(不与点A,B重合),点D是弧AC的中点,延长CD交经过点A的切线于点E,连接AD,当△ADE是等腰三角形时,求∠BAC的度数.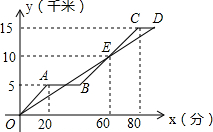 小明与小英同时从人们广场出发,沿同一路线骑自行车匀速前往净月潭公园,小明骑行20分钟后因事耽误一会儿,事后继续按原速骑行到达目的地.在小明和小英骑行过程中,二人骑行的路程y(千米)与小英的骑行时间x(分)之间的函数图象如图所示.
小明与小英同时从人们广场出发,沿同一路线骑自行车匀速前往净月潭公园,小明骑行20分钟后因事耽误一会儿,事后继续按原速骑行到达目的地.在小明和小英骑行过程中,二人骑行的路程y(千米)与小英的骑行时间x(分)之间的函数图象如图所示.