题目内容
1．甲、乙两港分别位于长江的上、下游，相距s km，若一艘游轮在静水中的速度为a km/h，水流速度为b km/h，（b＜a）．则该游轮往返两港口所需的时间相差多少？分析 游轮逆水行驶的速度为（a-b）km/h，顺水行驶的速度为（a+b）km/h，再利用速度公式表示出它们行驶skm所用的时间，然后求它们的差即可．
解答 解：该游轮往返两港口所需的时间差为：$\frac{s}{a-b}$-$\frac{s}{a+b}$=$\frac{2bs}{{a}^{2}-{b}^{2}}$（h）．
点评 本题考查了列代数式（分式）：把问题中与数量有关的词语，用含有数字、字母和运算符号的式子表示出来，就是列代数式． 列代数式五点注意：①仔细辨别词义． ②分清数量关系． ③注意运算顺序．④规范书写格式．⑤正确进行代换．
练习册系列答案
相关题目
如图，已知a⊥b，b⊥c，c⊥d，求证：a⊥d．
如图，在四边形ABCD中，AD∥BC，AE平分∠BAD交DC于点E，且点E恰好为DC的中点．求证：BE⊥AE，BE平分∠ABC．
19．
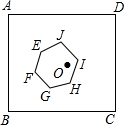如图，正方形ABCD的边长为1，中心为点O，有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转，在旋转过程中，这个正六边形始终在正方形ABCD内（包括正方形的边），当这个六边形的边长最大时，AE的最小值为（ ）
如图，正方形ABCD的边长为1，中心为点O，有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转，在旋转过程中，这个正六边形始终在正方形ABCD内（包括正方形的边），当这个六边形的边长最大时，AE的最小值为（ ）| A． | $\frac{\sqrt{2}+1}{2}$ | B． | $\frac{\sqrt{2}-1}{2}$ | C． | $\frac{3+2\sqrt{3}}{6}$ | D． | $\frac{3-2\sqrt{3}}{6}$ |