题目内容
13．分式方程$\frac{m}{x-1}$-$\frac{2}{x-1}$=$\frac{3}{{x}^{2}-2}$无解，则m的值为2．分析 首先求得使分母等于0的x的值，然后把方程去分母化成整式方程，把x的值代入即可求得m的值．
解答 解：当（x-1）（x2-2）=0时，x=1或±$\sqrt{2}$．
方程两边同时乘以（x-1）（x2-2）得：（m-2）（x2-2）=3（x-1）．
把x=1代入得：2-m=0，
解得：m=2．
把x=$\sqrt{2}$代入得：方程不成立；
把x=-$\sqrt{2}$代入，方程不成立．
总之，m=2．
故答案是：2．
点评 本题考查了分式方有解的条件，所求的x的值必须使方程的分母不等于0，因而解分式方程时必须进行检验．
练习册系列答案
相关题目
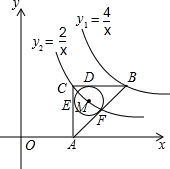如图，在平面直角坐标系中，点O为坐标原点，△ABC是直角三角形，∠ACB=90°，点B、C都在第一象限内，CA⊥x轴，垂足为点A，反比例函数y1=$\frac{4}{x}$的图象经过点B；反比例函数y2=$\frac{2}{x}$的图象经过点C（$\sqrt{2}$，m）．
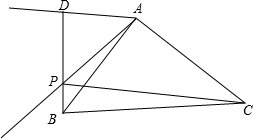在△ABC中，∠BAC=90°，作∠DAP=∠ABC=45°，过点B作BD⊥AD，垂足为D，BD交直线AP于P．
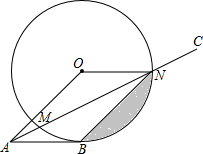如图，AB切⊙O于点B，AC交⊙O于点M、N，若四边形OABN恰为平行四边形，且弦BN的长为10cm．
如图，△ABC中，BF是高，延长CB至点D，使BD=BA，连接AD，过点D作DE⊥AB交AB的延长线于点E，当AF=BE，∠CAD=96°时，∠C=56°．