题目内容
12.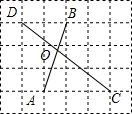 如图,在每个单位格线长为1的网格图中,A、B、C、D是四个格点,AB、CD相交于点O.则OD=2;△AOC的面积=$\frac{9}{10}$.
如图,在每个单位格线长为1的网格图中,A、B、C、D是四个格点,AB、CD相交于点O.则OD=2;△AOC的面积=$\frac{9}{10}$.
分析 先根据勾股定理求出CD的长,再由BD∥AC可得出△OBD∽△OAC,再由相似三角形的性质即可得出结论.
解答 解:由图可知,CD=$\sqrt{{3}^{2}+{4}^{2}}$=5.
∵BD∥AC,
∴△OBD∽△OAC,
∴$\frac{OD}{OC}$=$\frac{BD}{AC}$,即$\frac{OD}{5-OD}$=$\frac{2}{3}$,解得OD=2.
∵$\frac{OD}{OC}$=$\frac{2}{5}$,
∴△AOC的高=$\frac{1}{2}$×$\frac{3}{5}$×3=$\frac{9}{10}$.
故答案为:$\frac{9}{10}$.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形对应边的比等于相似比是解答此题的关键.

练习册系列答案
相关题目
2.张明同学的身高为1.6米,某一时刻他在阳光下的影长为2米,与他邻近一棵树的影长为8米,则这棵树的高是( )米.
| A. | 10 | B. | 6.4 | C. | 4 | D. | 无法确定 |
4.一个三角形的两边长为3和6,第三边的长是方程(x-3)(x-4)=0的根,则这个三角形第三边的长是( )
| A. | 3 | B. | 4 | C. | 3或4 | D. | 3和4 |
 如图,AD,AE是△ABC的∠BAC的内、外角平分线,过B作AD的垂线交AD的延长线于F,连FC并延长交AE于M,求证:AM=ME.
如图,AD,AE是△ABC的∠BAC的内、外角平分线,过B作AD的垂线交AD的延长线于F,连FC并延长交AE于M,求证:AM=ME.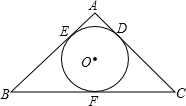 如图,△ABC的面积为4cm2,周长为10cm,求△ABC的内切圆半径.
如图,△ABC的面积为4cm2,周长为10cm,求△ABC的内切圆半径.