题目内容
17.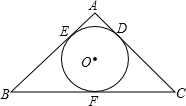 如图,△ABC的面积为4cm2,周长为10cm,求△ABC的内切圆半径.
如图,△ABC的面积为4cm2,周长为10cm,求△ABC的内切圆半径.
分析 连OA,OB,OC.把三角形ABC分成三个三角形,根据内心的性质和三角形面积公式用三个三角形的面积的和表示三角形ABC面积,从而可求得△ABC的内切圆半径.
解答 解:连OA,OB,OC.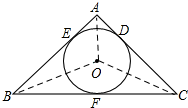
∵S△ABC=S△AOB+S△OBC+S△OAC,
∴$\frac{1}{2}$AB•r+$\frac{1}{2}$BC•r+$\frac{1}{2}$AC•r=4.
∴$\frac{1}{2}r$(AB+BC+AC)=4,即$\frac{1}{2}×10×r$=4.
解得:r=$\frac{4}{5}$cm.
答:△ABC的内切圆半径为$\frac{4}{5}$cm.
点评 本题主要考查的是三角形的内心,明确三角形的面积=$\frac{1}{2}×$三角形的周长×内切圆半径是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列各数中,比-1小的数是( )
| A. | 0 | B. | 1 | C. | -100 | D. | 2 |
5.学校举行红歌赛,全校21个班级均组队参赛.所有参赛代表队的成绩互不相同,小敏在已知自己班级代表队成绩的情况下,要想知道本班代表队是否进入前10名,只需要知道所有参赛代表队成绩的( )
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
2. 某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
 某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )| A. |  | B. |  | C. |  | D. |  |
6.下列图形中内角和等于360°的是( )
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
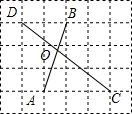 如图,在每个单位格线长为1的网格图中,A、B、C、D是四个格点,AB、CD相交于点O.则OD=2;△AOC的面积=$\frac{9}{10}$.
如图,在每个单位格线长为1的网格图中,A、B、C、D是四个格点,AB、CD相交于点O.则OD=2;△AOC的面积=$\frac{9}{10}$. 如图是一盘中国象棋残局的一部分,以“帅”为原点建立坐标系,知道“兵”所在位置的坐标是(2,3),则“炮”所在位置的坐标是(-3,2).
如图是一盘中国象棋残局的一部分,以“帅”为原点建立坐标系,知道“兵”所在位置的坐标是(2,3),则“炮”所在位置的坐标是(-3,2). 如图,已知Rt△ABC≌Rt△DEC,连结AD,若∠1=25°,则∠B的度数是70°.
如图,已知Rt△ABC≌Rt△DEC,连结AD,若∠1=25°,则∠B的度数是70°.