题目内容
20. 如图,AD,AE是△ABC的∠BAC的内、外角平分线,过B作AD的垂线交AD的延长线于F,连FC并延长交AE于M,求证:AM=ME.
如图,AD,AE是△ABC的∠BAC的内、外角平分线,过B作AD的垂线交AD的延长线于F,连FC并延长交AE于M,求证:AM=ME.
分析 延长BF,AC交于H,根据角平分线的定义和平角的定义得到∠FAE=90°,推出BF∥AE,于是得到△ACM∽△CFH,△BCF∽△CME,根据相似三角形的性质得到$\frac{AM}{FH}=\frac{CM}{CF}$,$\frac{ME}{BF}=\frac{CM}{CF}$,等量代换得到$\frac{AM}{FH}=\frac{ME}{BF}$,通过△ABF≌△AHF,得到BF=FH,于是求得结论.
解答 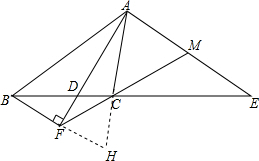 证明:延长BF,AC交于H,
证明:延长BF,AC交于H,
∵AD、AE分别是△ABC的∠BAC内外角平分线,
∴∠FAE=90°,
∵BF⊥AD,
∴BF∥AE,
∴△ACM∽△CFH,△BCF∽△CME,
∴$\frac{AM}{FH}=\frac{CM}{CF}$,$\frac{ME}{BF}=\frac{CM}{CF}$,
∴$\frac{AM}{FH}=\frac{ME}{BF}$,
∵AD是∠BAC的平分线,且是BH边上的垂线,
∴∠BAF=∠HAF,∠AFB=∠AFH,
在△ABF与△AHF中,$\left\{\begin{array}{l}{∠BAF=∠HAF}\\{AD=AD}\\{∠AFB=∠AFH}\end{array}\right.$,
∴△ABF≌△AHF,
∴BF=FH,
∴AM=ME.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,角平分线的定义,正确的作出辅助线是解题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
8.下列各数中,比-1小的数是( )
| A. | 0 | B. | 1 | C. | -100 | D. | 2 |
15.在△ABC中,∠C=90°,AB=2,AC=1,则cosB的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
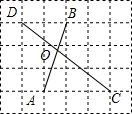 如图,在每个单位格线长为1的网格图中,A、B、C、D是四个格点,AB、CD相交于点O.则OD=2;△AOC的面积=$\frac{9}{10}$.
如图,在每个单位格线长为1的网格图中,A、B、C、D是四个格点,AB、CD相交于点O.则OD=2;△AOC的面积=$\frac{9}{10}$. 如图是一盘中国象棋残局的一部分,以“帅”为原点建立坐标系,知道“兵”所在位置的坐标是(2,3),则“炮”所在位置的坐标是(-3,2).
如图是一盘中国象棋残局的一部分,以“帅”为原点建立坐标系,知道“兵”所在位置的坐标是(2,3),则“炮”所在位置的坐标是(-3,2).