题目内容
7．函数y=-2x2+4x中自变量x的取值范围是全体实数．分析 根据当函数表达式是整式时，自变量可取全体实数，可得答案．
解答 解：∵函数表达式是整式，
∴函数自变量的取值范围是全体实数．
故答案为：全体实数．
点评 本题主要考查的是函数自变量的取值范围，明确函数表达式是整式时，自变量可取全体实数是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
17．在Rt△ABC中，∠C=90°，则下列等式成立的是（ ）
| A． | AB=AC×sinB | B． | BC=AB×sinB | C． | BC=AC×tanB | D． | BC=AC×tanA |
15．在△ABC中，∠C=90°，AB=2，AC=1，则cosB的值是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 2 |
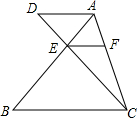如图，AD∥FE∥CB．试探究S△ADC，S△AEC，S△ABC之间的关系，并证明结论．
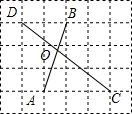如图，在每个单位格线长为1的网格图中，A、B、C、D是四个格点，AB、CD相交于点O．则OD=2；△AOC的面积=$\frac{9}{10}$．
19．下列关于x的方程中，没有实数根的是（ ）
| A． | 3x2+4x-2=0 | B． | 2x2+5=6x | C． | 3x2-2$\sqrt{6}$x+2=0 | D． | 2x2+mx-1=0 |
如图，已知BD是∠ABC的角平分线，DE⊥AB于E点，AB=14cm，BC=12cm，S△ABC=52cm2，则DE=4cm．