题目内容
13.已知变量y与x的关系满足下表,那么能反映y与x之间的函数关系的解析式是( )| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 4 | 3 | 2 | 1 | 0 | … |
| A. | y=-2x | B. | y=x+4 | C. | y=-x+2 | D. | y=2x-2 |
分析 设y与x之间的函数关系的解析式是y=kx+b(k≠0),然后将表格中两组数据代入求解即可.
解答 解:设y与x之间的函数关系的解析式是y=kx+b(k≠0),
则$\left\{\begin{array}{l}{k+b=1}\\{b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
所以,y与x之间的函数关系的解析式是y=-x+2.
故选C.
点评 本题考查了待定系数法求一次函数解析式,待定系数法是求函数解析式常用的方法之一,需要熟练掌握.

练习册系列答案
相关题目
2.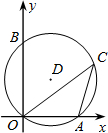 如图,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为$\widehat{OBA}$上的一点(不与O、A两点重合),连接OC,AC,则cosC的值为( )
如图,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为$\widehat{OBA}$上的一点(不与O、A两点重合),连接OC,AC,则cosC的值为( )
 如图,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为$\widehat{OBA}$上的一点(不与O、A两点重合),连接OC,AC,则cosC的值为( )
如图,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为$\widehat{OBA}$上的一点(不与O、A两点重合),连接OC,AC,则cosC的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
3.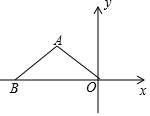 如图,已知等腰△ABO的底边BO在x轴上,且BO=8,AB=AO=5,点A的坐标是( )
如图,已知等腰△ABO的底边BO在x轴上,且BO=8,AB=AO=5,点A的坐标是( )
 如图,已知等腰△ABO的底边BO在x轴上,且BO=8,AB=AO=5,点A的坐标是( )
如图,已知等腰△ABO的底边BO在x轴上,且BO=8,AB=AO=5,点A的坐标是( )| A. | (-3,4) | B. | (3,-4) | C. | (-4,3) | D. | (4,-3) |
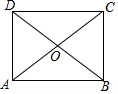 如图,在矩形ABCD中,对角线AC、BD相交于点O,且OA=OD.若∠OAD=50°,求∠OAB的度数.
如图,在矩形ABCD中,对角线AC、BD相交于点O,且OA=OD.若∠OAD=50°,求∠OAB的度数.