题目内容
10. 已知如图,长方形ABCD中,有一内接?EFGH,它的各边平行于对角线,若长方形对角线长为12cm,则?EFGH的周长为24cm.
已知如图,长方形ABCD中,有一内接?EFGH,它的各边平行于对角线,若长方形对角线长为12cm,则?EFGH的周长为24cm.
分析 延长HG交BC的延长线于点K,根据平行四边形的性质得出EH=GF,∠AEH=∠ABD=∠BDC=∠CGF,再由AAS定理得出△AEH≌△CGF(AAS),故可得出AH=CF,同理可得出△FCG≌△KCG,故可得出FG=GK,根据HG+FG=HG+GK=HK=AC即可得出结论.
解答 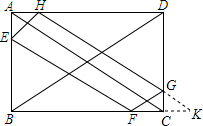 解:延长HG交BC的延长线于点K
解:延长HG交BC的延长线于点K
∵四边形EFGH是平行四边形,
∴EH=GF,且有EH∥BD∥GF,
∴∠AEH=∠ABD=∠BDC=∠CGF,
在△AEH与△CGF中,
$\left\{\begin{array}{l}∠AEH=∠CGF\\∠EAH=∠GCF\\ EH=GF\end{array}\right.$,
∴△AEH≌△CGF(AAS),
∴AH=CF.
在四边形ACKH中,
∵AH∥CK,AC∥HK,
∴四边形ACKH是平行四边形,
∴AH=CK.
在△FCG和△KCG中,
$\left\{\begin{array}{l}CG=CG\\∠FCG=∠KCG\\ CF=CK\end{array}\right.$,
∴△FCG≌△KCG(SAS),
∴FG=GK,
∴HG+FG=HG+GK=HK=AC,
∴平行四边形EFGH的周长为:2(HG+FG)=2AC=24(cm).
故答案为:24.
点评 本题考查的是平行四边形的性质,根据题意作出辅助线,构造出全等三角形,利用全等三角形的对应边相等即可得出结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.在平面直角坐标系中,正方形OABC的顶点A坐标为(2,1),点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
| A. | -$\sqrt{5}$ | B. | -2 | C. | 2 | D. | $\sqrt{5}$ |
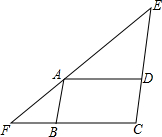 如图,在△EFC中,点A是EF上一点,且AD∥CF,AB∥CE,∠EAD=∠BAF.
如图,在△EFC中,点A是EF上一点,且AD∥CF,AB∥CE,∠EAD=∠BAF. 已知?ABCD的两条对角线相交于点O,AB=5,BC=5,BD=8,求?ABCD的周长与面积.
已知?ABCD的两条对角线相交于点O,AB=5,BC=5,BD=8,求?ABCD的周长与面积.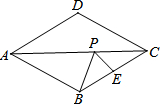 如图,在菱形ABCD中,AD=6,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为3$\sqrt{3}$.
如图,在菱形ABCD中,AD=6,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为3$\sqrt{3}$.