题目内容
18.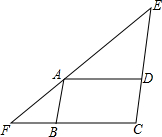 如图,在△EFC中,点A是EF上一点,且AD∥CF,AB∥CE,∠EAD=∠BAF.
如图,在△EFC中,点A是EF上一点,且AD∥CF,AB∥CE,∠EAD=∠BAF.(1)求证:CE=CF;
(2)如果CE=6cm,求?ABCD的周长.
分析 (1)直接利用平行线的性质得出∠F=∠EAD,∠E=∠FAB,进而得出∠E=∠F,即可得出答案;
(2)直接利用(1)中所求,得出FB=AB,AD=DE,CE=FC,即可得出答案.
解答 (1)证明:∵AD∥CF,AB∥CE,
∴∠F=∠EAD,∠E=∠FAB,
∵∠EAD=∠BAF,
∴∠E=∠F,
∴FC=EC;
(2)解:由(1)可得:∠F=∠EAD=∠E=∠FAB,
则FB=AB,AD=DE,CE=FC,
∵CE=6cm,
∴?ABCD的周长为:6+6=12(cm).
点评 此题主要考查了平行线的性质以及平行四边形的性质,得出∠E=∠F是解题关键.

练习册系列答案
相关题目
6.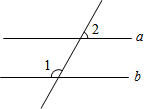 如图,已知a∥b,∠1=115°,则∠2的度数是( )
如图,已知a∥b,∠1=115°,则∠2的度数是( )
 如图,已知a∥b,∠1=115°,则∠2的度数是( )
如图,已知a∥b,∠1=115°,则∠2的度数是( )| A. | 45° | B. | 55° | C. | 65° | D. | 85° |
8.函数$y=(a-2){x^{{a^2}-2}}$是反比例函数,则a的值是( )
| A. | 1或-1 | B. | -2 | C. | 2 | D. | 2或-2 |
 已知关于x的一元二次方程x2$+2x+\frac{k-1}{2}=0$有两个不相等的实数根,k为正整数.
已知关于x的一元二次方程x2$+2x+\frac{k-1}{2}=0$有两个不相等的实数根,k为正整数.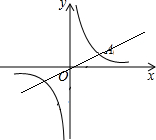 已知一次函数y=kx与反比例函数y=$\frac{3}{x}$的图象都经过点A(m,1).求:
已知一次函数y=kx与反比例函数y=$\frac{3}{x}$的图象都经过点A(m,1).求: 已知如图,长方形ABCD中,有一内接?EFGH,它的各边平行于对角线,若长方形对角线长为12cm,则?EFGH的周长为24cm.
已知如图,长方形ABCD中,有一内接?EFGH,它的各边平行于对角线,若长方形对角线长为12cm,则?EFGH的周长为24cm.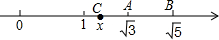 如图,数轴上与$\sqrt{3}、\sqrt{5}$对应的点分别是A,B,点C也在数轴上,且AB=AC,设点C表示的数为x
如图,数轴上与$\sqrt{3}、\sqrt{5}$对应的点分别是A,B,点C也在数轴上,且AB=AC,设点C表示的数为x