题目内容
4.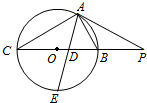 如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠CAB的平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠CAB的平分线与BC和圆O分别交于点D和E.(1)求证:$\frac{AB}{AC}$=$\frac{PA}{PC}$;
(2)求AD•AE的值.
分析 (1)根据已知条件得到△PAB∽△PCA,于是得到结论;
(2)由切割线定理求出PC=40,BC=30,根据已知条件推出△ACE∽△ADB,列比例式即可得到结果.
解答 解:(1)∵PA为圆O的切线,
∴∠PAB=∠ACP,
∵∠P=∠P,
∴△ABP∽△PAC,
∴$\frac{AB}{AC}$=$\frac{PA}{PC}$;
(2)连接AO,CE.
∵PA为圆O的切线,PBC是过点O的割线,
∴PA2=PB•PC,
∵PA=10,PB=5,
∴PC=$\frac{P{A}^{2}}{PB}$=$\frac{1{0}^{2}}{5}$,
∴PC=20,
∴BC=15,
∵∠CAB=90°,
∴AC2+AB2=BC2=225,
由(1)知$\frac{AB}{AC}=\frac{PA}{PC}=\frac{1}{2}$,
∴AC=6$\sqrt{5}$,AB=3$\sqrt{5}$,
∵AE平分∠CAB,
∴∠CAE=∠EAB,
∠E=∠ABD,
∴△ACE∽△ADB,
∴$\frac{AB}{AE}=\frac{AD}{AC}$,
∴AD•AE=AB•AC=3$\sqrt{5}$×$6\sqrt{5}$=90.
点评 本题考查了切线的性质,切割线定理,相似三角形的判定和性质,正确的作出辅助线构造相似三角形是解题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
19.已知二次函数y=-$\frac{1}{2}$(x-h)2+3,当x>-2时,y随x的增大而减小,则有( )
| A. | h≥-2 | B. | h≤-2 | C. | h>-2 | D. | h<-2 |
9.若|a|=8,|b|=6,且|a+b|=a+b,那么a-b的值只能是( )
| A. | 2 | B. | 14 | C. | 6 | D. | 2或14 |