题目内容
10.若m+n-p=0,则$m(\frac{1}{n}-\frac{1}{p})+n(\frac{1}{m}-\frac{1}{p})-p(\frac{1}{m}+\frac{1}{n})$的值是( )| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
分析 先根据题意把原式化为$\frac{m-p}{n}$+$\frac{n-p}{m}$-$\frac{m+n}{p}$的形式,再由m+n-p=0得出m-p=-n,m-p=-n,n-p=-m,m+n=p,代入原式进行计算即可.
解答 解:原式=$\frac{m}{n}$-$\frac{m}{p}$+$\frac{n}{m}$-$\frac{n}{p}$-$\frac{p}{m}$-$\frac{p}{n}$
=$\frac{m-p}{n}$+$\frac{n-p}{m}$-$\frac{m+n}{p}$,
∵m+n-p=0,
∴m-p=-n,m-p=-n,n-p=-m,m+n=p,
∴原式=-1-1-1=-3.
故选A.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知3m2-2m-5=0,5n2+2n-3=0,其中m,n为实数,则|m-$\frac{1}{n}$|=( )
| A. | 0 | B. | $\frac{8}{3}$ | C. | $\frac{5}{3}$ | D. | 0或$\frac{8}{3}$ |
18.某中学举行书法比赛,各年龄组的参赛人数如下表所示:
则全体参赛选手年龄的平均数和中位数分别为( )
| 年龄组 | 13岁 | 14岁 | 15岁 | 16岁 |
| 参赛人数 | 9 | 15 | 3 | 3 |
| A. | 14.5,14.5 | B. | 14,15 | C. | 14.5,14 | D. | 14,14 |
2.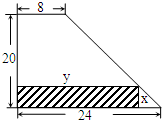 某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )
 某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )| A. | x=15,y=12 | B. | x=12,y=15 | C. | x=14,y=10 | D. | x=10,y=14 |
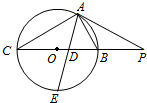 如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠CAB的平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠CAB的平分线与BC和圆O分别交于点D和E.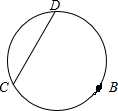 如图,已知CD是圆中的弦,B为圆上一点,且$\widehat{BC}$=$\widehat{BD}$.
如图,已知CD是圆中的弦,B为圆上一点,且$\widehat{BC}$=$\widehat{BD}$.