题目内容
13.判断以线段a,b,c为边构成的三角形是不是直角三角形,其中a=$\sqrt{6}$,b=1,c=$\sqrt{5}$.解因为a2+b2=($\sqrt{6}$)2+1=7,c2=($\sqrt{5}$)2=5,a2+b2≠c2.
所以由a,b,c构成的三角形不是直角三角形.以上解答是否正确?如不正确,给出正确解答.
分析 根据勾股定理的逆定理,求出两小边的平方和和大边的平方,看看是否相等即可.
解答 解:以上解答不正确,理由如下:
∵c2+b2=($\sqrt{5}$)2+1=6,a2=($\sqrt{6}$)2=6,
c2+b2=a2.
∴由a,b,c构成的三角形是直角三角形.
点评 本题考查了勾股定理的逆定理的应用,注意:如果两边(两小边)的平方和等于第三边(大边)的平方,那么这个三角形是直角三角形.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
3.以下说法正确的是( )
| A. | 有公共顶点,并且相等的两个角是对顶角 | |
| B. | 两条直线相交,任意两个角都是对顶角 | |
| C. | 实数与数轴上的点是一一对应的 | |
| D. | 过一点有且只有一条直线与已知直线平行 |
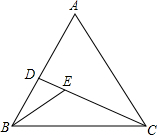 如图,在等边△ABC中,D在边AB上,E在CD上,∠BED=60°,DE=2,△ACD的面积6$\sqrt{3}$,则线段CD的长为6.
如图,在等边△ABC中,D在边AB上,E在CD上,∠BED=60°,DE=2,△ACD的面积6$\sqrt{3}$,则线段CD的长为6.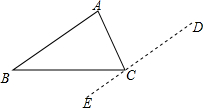 请根据图给出的图示(过点C作ED∥AB),对“三角形内角和等于180°”说理.(作平行线是把角从一个位置“转移”到另一个位置的重要手段)
请根据图给出的图示(过点C作ED∥AB),对“三角形内角和等于180°”说理.(作平行线是把角从一个位置“转移”到另一个位置的重要手段)