题目内容
7.已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),$\frac{BC}{AC}$=$\frac{3}{4}$,(1)求直线AB的解析式;
(2)在x轴上确定一点D,连接DB,使得△ADB与△ABC相似,并求出点D的坐标;
(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m使得△APQ与△ADB相似?如存在,请直接写出m的值;如不存在,请说明理由.

分析 (1)先根据A(-3,1),C(1,0),求出AC进而得出BC=3求出B点坐标,利用待定系数法求出直线AB的解析式即可;
(2)运用相似三角形的性质就可求出点D的坐标;
(3)①由于△APQ与△ADB已有一组公共角相等,只需分△APQ∽△ABD和△APQ∽△ADB两种情况讨论,然后运用相似三角形的性质建立关于m的方程,就可解决问题,
②当点D和C重合时,同①的方法可得;
解答 解:(1)∵A(-3,0),C(1,0),
∴AC=4,
∵$\frac{BC}{AC}=\frac{3}{4}$,
∴BC=$\frac{3}{4}$×4=3,
∴B(1,3),
设直线AB的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-3k+b=0}\\{k+b=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=\frac{9}{4}}\end{array}\right.$,
∴直线AB的解析式为y=$\frac{3}{4}$x+$\frac{9}{4}$
(2)若△ADB与△ABC相似,
①当点D与C重合时,△ADB∽△ABC,此时D(1,0),
②过点B作BD⊥AB交x轴于D,∴∠ABD=∠ACB=90°,如图1,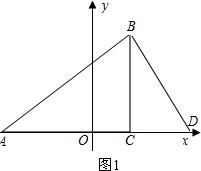
此时$\frac{AB}{AC}=\frac{AD}{AB}$,即AB2=AC•AD.
∵∠ACB=90°,AC=4,BC=3,
∴AB=5,
∴25=4AD,
∴AD=$\frac{25}{4}$,
∴OD=AD-AO=$\frac{25}{4}$-3=$\frac{13}{4}$,
∴点D的坐标为($\frac{13}{4}$,0).即:符合条件的D($\frac{13}{4}$,0)和(1,0)
(3)∵AP=DQ=m,
∴AQ=AD-QD=$\frac{25}{4}$-m.
Ⅰ、若△APQ∽△ABD,如图2,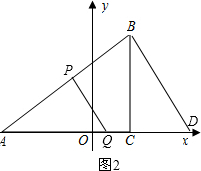
则有$\frac{AP}{AB}=\frac{AQ}{AD}$,
∴AP•AD=AB•AQ,
∴$\frac{25}{4}$m=5($\frac{25}{4}$-m),
解得m=$\frac{25}{9}$.
Ⅱ、若△APQ∽△ADB,如图3,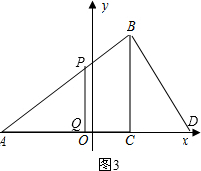
则有$\frac{AP}{AD}=\frac{AQ}{AB}$,
∴AP•AB=AD•AQ,
∴5m=$\frac{25}{4}$($\frac{25}{4}$-m),
解得:m=$\frac{125}{36}$,
②当点D与C重合时,可得m=$\frac{16}{9}$或m=$\frac{20}{9}$.
综上所述:符合要求的m的值为$\frac{25}{9}$或$\frac{125}{36}$或$\frac{16}{9}$或$\frac{20}{9}$.
点评 此题是相似形综合题,主要考查了是待定系数法,涉及到相似三角形的判定与性质、勾股定理等知识,考查了分类讨论的数学思想,属于中档题,解本题的关键是关键相似建立方程求解.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案| A. | 0.306×10-3米 | B. | 3.06×10-3米 | C. | 30.6×10-14米 | D. | 3.06×10-13米 |
(1)若A、B、C、D、E是平面内不同的5个点,则过这5个点的直线可能有多少条?要求确定出可能的条数,并画出每种情况的一种简图;
(2)平面内有n(n为不小于2的整数)个点,过这n个点最多能作多少条直线?完成下列表格.
| 点的个数 | 2 | 3 | 4 | 5 | … | 2016 | … | n |
| 能做直线最多条数 | 1 | 3 | 6 | / | … | 2031120 | … | $\frac{n(n-1)}{2}$ |
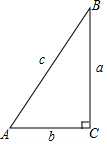 如图,在Rt△ABC中,∠C=90°,若a=4,c=5,则tanA=$\frac{4}{3}$.
如图,在Rt△ABC中,∠C=90°,若a=4,c=5,则tanA=$\frac{4}{3}$.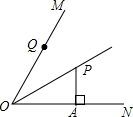 如图,OP平分∠MON,PA⊥ON,垂足为A,OA=8,PA=6,Q是射线OM上的一个动点,则线段PQ的最小值是( )
如图,OP平分∠MON,PA⊥ON,垂足为A,OA=8,PA=6,Q是射线OM上的一个动点,则线段PQ的最小值是( )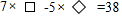 老师在课下给同学们留了如图所示的一个等式,让同学自己出题,并作出答案,请你回答处下列两个同学所提出问题的答案.
老师在课下给同学们留了如图所示的一个等式,让同学自己出题,并作出答案,请你回答处下列两个同学所提出问题的答案.