题目内容
20.已知反比例函数y=$\frac{3}{x}$,当1<x<3时,y的取值范围是( )| A. | 0<y<3 | B. | 1<y<3 | C. | y>1 | D. | y>3 |
分析 根据反比例函数的增减性可求得答案.
解答 解:
在反比例函数y=$\frac{3}{x}$中,k=3>0,
∴函数图象在第一、三象限,且在每个象限内y随x的增大而减小,
当1<x<3时,函数图象在第一象限,
当x=3时,y=1,当x=1时,y=3,
∴1<y<3,
故选B.
点评 本题主要考查反比例函数的增减性,掌握反比例函数的增减性是解题的关键,即在y=$\frac{k}{x}$(k≠0)中,当k>0时,在每个象限内y随x的增大而减小,当k<0时,在每个象限内y随x的增大而增大.

练习册系列答案
相关题目
5.如果点(-2,3)在反比例函数y=$\frac{k}{x}$(k≠0的常数)的图象上,那么对于反比例函数y=$\frac{k}{x}$下列说法正确的是( )
| A. | 在每一象限内,y随x的增大而增大 | B. | 在每一象限内,y随x的增大而减小 | ||
| C. | y恒为正值 | D. | y恒为负值 |
10. 乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )
乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )
 乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )
乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )| A. | 1.5小时 | B. | 1.8小时 | C. | 2小时 | D. | 2.5小时 |
 如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项.
如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项.
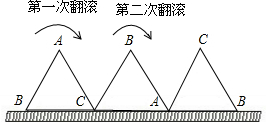 一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.
一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.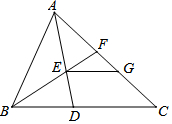 如图,△ABC中,∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG∥BC交AC于点G.
如图,△ABC中,∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG∥BC交AC于点G.