题目内容
7.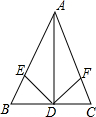 如图,在△ABC中,AB=AC,D为BC中点,DE、DF分别是∠ADB、∠ADC的平分线,若DE=2,求DF的长.
如图,在△ABC中,AB=AC,D为BC中点,DE、DF分别是∠ADB、∠ADC的平分线,若DE=2,求DF的长.
分析 证明△ADE≌△ADF即可,然后可得DF=DE=2.
解答 解:如图,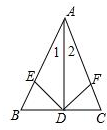
∵AB=AC,D为BC中点,
∴∠ADB=∠ADC=90°,∠1=∠2,
∵DE、DF分别是∠ADB,∠ADC的平分线,
∴∠ADE=$\frac{1}{2}$∠ADB=45°,∠ADF=$\frac{1}{2}$∠ADC=45°,
∴∠ADE=∠ADF,
在△ADE和△ADF中,
$\left\{\begin{array}{l}{∠1=∠2}\\{AD=AD}\\{∠ADE=∠ADF}\end{array}\right.$,
∴△ADE≌△ADF(ASA),
∴DF=DE=2.
点评 本题考查了等腰三角形三线合一的性质、全等三角形的判定与性质,比较基础.对于全等三角形的证明,差什么条件就去寻找什么条件,如果条件不是明显的,则先通过推导得出所需要的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.设A(1,y1),B(2,y2)是抛物线y=-(x+1)2+m上的两点,则y1,y2的大小关系为( )
| A. | y1≤y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1>y2 |
19.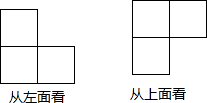 一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.
一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.
 一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.
一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.| A. | 4个 | B. | 5个 | C. | 6个 | D. | 无法确定 |
 如图所示,已知AC、BD相交于点O,OC=OA,OB=OD,则图中全等的三角形有4对.
如图所示,已知AC、BD相交于点O,OC=OA,OB=OD,则图中全等的三角形有4对.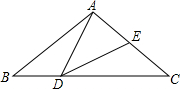 如图,在△ABC中,AB=AC=2,点D在线段BC上运动(点D不与B、C重合),∠B=40°,连结AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,点D在线段BC上运动(点D不与B、C重合),∠B=40°,连结AD,作∠ADE=40°,DE交线段AC于E.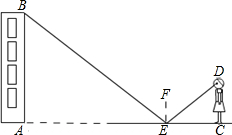 小玲用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=25米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米.请你帮助小玲计算出教学大楼的高度AB是多少米(注意:根据光的反射定律:反射角等于入射角).
小玲用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=25米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米.请你帮助小玲计算出教学大楼的高度AB是多少米(注意:根据光的反射定律:反射角等于入射角).