题目内容
15.设A(1,y1),B(2,y2)是抛物线y=-(x+1)2+m上的两点,则y1,y2的大小关系为( )| A. | y1≤y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1>y2 |
分析 根据抛物线的性质,抛物线上的点离对称轴越远,对应的函数值就越小,由x取-3、0、1时,x取0时所对应的点离对称轴最近,x取-3与1时所对应的点离对称轴一样近,即可得到答案.
解答 解:∵抛物线y=-(x+1)2+m开口向下,对称轴是直线x=-1,
∴抛物线上的点离对称轴越远,对应的函数值就越小,
∵x取2时所对应的点离对称轴远,x取1时所对应的点离对称轴近,
∴y1>y2.
故选D.
点评 本题考查了二次函数图象上点的坐标特征.解题时,需熟悉抛物线的有关性质:抛物线的开口向下,则抛物线上的点离对称轴越远,对应的函数值就越小.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,在△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,且DE=3cm,∠BAC=60°,则BC=9cm.
如图,在△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,且DE=3cm,∠BAC=60°,则BC=9cm.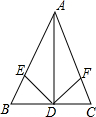 如图,在△ABC中,AB=AC,D为BC中点,DE、DF分别是∠ADB、∠ADC的平分线,若DE=2,求DF的长.
如图,在△ABC中,AB=AC,D为BC中点,DE、DF分别是∠ADB、∠ADC的平分线,若DE=2,求DF的长.