题目内容
12.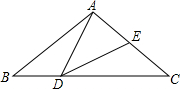 如图,在△ABC中,AB=AC=2,点D在线段BC上运动(点D不与B、C重合),∠B=40°,连结AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,点D在线段BC上运动(点D不与B、C重合),∠B=40°,连结AD,作∠ADE=40°,DE交线段AC于E.(1)当∠ADB=115°时,∠DEC=115°.
(2)在D运动过程中,有没有可能使得△ABD与△DCE全等?如有可能,求出CD的长度;如没有可能,请说明理由.
(3)若△ADE是等腰三角形,求∠BAD的大小.
分析 (1)利用邻补角的性质和三角形内角和定理解题;
(2)当DC=2时,利用∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,求出∠ADB=∠DEC,再利用AB=DC=2,即可得出△ABD≌△DCE;
(3)分类谈论:①若AD=AE时;②若DA=DE时,③若EA=ED时,即可解题.
解答 解:(1)∵AB=AC,∠B=40°,
∴∠C=∠B=40°.
∵∠EDC=180°-∠ADB-∠ADE=180°-115°-40°=25°.
∴∠DEC=180°-40°-25°=115°.
故答案为:115;
(2)当DC=2时,△ABD≌△DCE,
理由:∵∠C=40°,
∴∠DEC+∠EDC=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC,
又∵AB=DC=2,
在△ABD和△DCE中,
$\left\{\begin{array}{l}∠ADB=∠DEC\\∠B=∠C\\ AB=DC\end{array}\right.$,
∴△ABD≌△DCE(AAS);
(3)∵AB=AC,
∴∠B=∠C=40°,
①若AD=AE时,则∠ADE=∠AED=40°,
∵∠AED>∠C,
∴△ADE不可能是等腰三角形;
②若DA=DE时,即∠DAE=∠DEA=$\frac{1}{2}$(180°-40°)=70°,
∵∠BAC=180°-40°-40°=100°,
∴∠BAD=100°-70°=30°;
③若EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°-40°=60°,
∴当∠BAD=30°或60°时,△ADE是等腰三角形.
点评 本题考查了全等三角形的判定与性质,考查了等腰三角形的判定和腰长相等的性质.运用分类讨论解本题是解题的关键.

练习册系列答案
相关题目
17.在-(-9),(-1)2013,-33,-|-2|中,负数共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,且DE=3cm,∠BAC=60°,则BC=9cm.
如图,在△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,且DE=3cm,∠BAC=60°,则BC=9cm.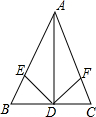 如图,在△ABC中,AB=AC,D为BC中点,DE、DF分别是∠ADB、∠ADC的平分线,若DE=2,求DF的长.
如图,在△ABC中,AB=AC,D为BC中点,DE、DF分别是∠ADB、∠ADC的平分线,若DE=2,求DF的长.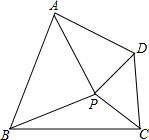 P为四边形ABCD内一点,如果△PAB和△PCD都是以AB,CD为底的等腰直角三角形,则该四边形称为“对底四边形”,AB,CD叫底.
P为四边形ABCD内一点,如果△PAB和△PCD都是以AB,CD为底的等腰直角三角形,则该四边形称为“对底四边形”,AB,CD叫底.