题目内容
 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周).
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周).(1)写出B点的坐标(
(2)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
考点:坐标与图形性质
专题:动点型
分析:(1)根据矩形的性质以及点的坐标的定义写出即可;
(2)根据矩形的性质以及点到x轴的距离等于纵坐标的长度求出OP,再根据时间=路程÷速度列式计算即可得解.
(2)根据矩形的性质以及点到x轴的距离等于纵坐标的长度求出OP,再根据时间=路程÷速度列式计算即可得解.
解答:解:(1)∵A点的坐标为(4,0),C点的坐标为(0,6),
∴OA=4,OC=6,
∴点B(4,6);
故答案为:(4,6).
(2)点P到x轴距离为5个单位长度时,点P的纵坐标为5,
若点P在OC上,则OP=5,
t=5÷2=2.5秒,
若点P在AB上,则OP=OC+BC+BP=6+4+(6-5)=11,
t=11÷2=5.5秒,
综上所述,点P移动的时间为2.5秒或5.5秒.
∴OA=4,OC=6,
∴点B(4,6);
故答案为:(4,6).
(2)点P到x轴距离为5个单位长度时,点P的纵坐标为5,
若点P在OC上,则OP=5,
t=5÷2=2.5秒,
若点P在AB上,则OP=OC+BC+BP=6+4+(6-5)=11,
t=11÷2=5.5秒,
综上所述,点P移动的时间为2.5秒或5.5秒.
点评:本题考查了坐标与图形性质,动点问题,主要利用了矩形的性质和点的坐标的确定,难点在于(2)要分情况讨论.

练习册系列答案
相关题目
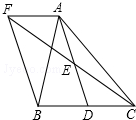 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF. 如图,AB是⊙O的直径,C是
如图,AB是⊙O的直径,C是
 如图,有一条小路穿过长方形的草地ABCD,若AB=30m,BC=42m,AE=50m,则这条小路的面积是多少?
如图,有一条小路穿过长方形的草地ABCD,若AB=30m,BC=42m,AE=50m,则这条小路的面积是多少? 如图,每相邻三个点构成的“∵”或“∴”,所形成的三角形都是正三角形,且每一个小正三角形的面积为1,这样的图叫做三角形格点图,这些多边形叫三角形格点多边形.
如图,每相邻三个点构成的“∵”或“∴”,所形成的三角形都是正三角形,且每一个小正三角形的面积为1,这样的图叫做三角形格点图,这些多边形叫三角形格点多边形.