题目内容
 如图,AB是⊙O的直径,C是
如图,AB是⊙O的直径,C是 |
| BD |
(1)求证:CF=BF;
(2)求证:CB2=CH•CA;
(3)若AH=5,当BH:AB=2:3时,CH=
考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)连接BC,根据圆周角定理求出∠CAB=∠CBD,根据三角形内角和定理求出∠CAB=∠BCE,推出∠CBF=∠BCF,即可得出答案;
(2)证△CBH∽△CAB即可;
(3)根据相似得出比例式,根据已知代入,即可得出答案.
(2)证△CBH∽△CAB即可;
(3)根据相似得出比例式,根据已知代入,即可得出答案.
解答:(1)证明:连接BC,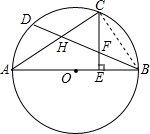
∵AB是⊙O直径,
∴∠ACB=90°,
∵CE⊥AB,
∴∠CEB=90°,
∴∠BDE+∠CBA=90°,∠CAB+∠CBA=90°,
∴∠BDE=∠CAB,
∵弧CD=弧BC,
∴∠CBF=∠CAB,
∴∠BCE=∠CBF,
∴CF=BF;
(2)证明:∵∠CBF=∠CAB,∠BCH=∠BCA,
∴△CBH∽△CAB,
∴
=
,
∴CB2=CH•CA;
(3)解:∵△CBH∽△CAB,BH:AB=2:3,AH=5,
∴
=
=
=
,
∴设CH=2x,BC=3x,
∴
=
,
x=2,
即CH=4,
故答案为:4.

∵AB是⊙O直径,
∴∠ACB=90°,
∵CE⊥AB,
∴∠CEB=90°,
∴∠BDE+∠CBA=90°,∠CAB+∠CBA=90°,
∴∠BDE=∠CAB,
∵弧CD=弧BC,
∴∠CBF=∠CAB,
∴∠BCE=∠CBF,
∴CF=BF;
(2)证明:∵∠CBF=∠CAB,∠BCH=∠BCA,
∴△CBH∽△CAB,
∴
| BC |
| CH |
| CA |
| BC |
∴CB2=CH•CA;
(3)解:∵△CBH∽△CAB,BH:AB=2:3,AH=5,
∴
| BH |
| AB |
| BC |
| AC |
| CH |
| BC |
| 2 |
| 3 |
∴设CH=2x,BC=3x,
∴
| 3x |
| 5+2x |
| 2 |
| 3 |
x=2,
即CH=4,
故答案为:4.
点评:本题考查了圆周角定理,相似三角形的性质和判定,等腰三角形的判定的应用,主要考查学生运用定理进行推理的能力,注意:在同圆中,等弧所对的圆周角相等,题目比较好,但是有一定的难度.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
电视机厂从2万台电视机中,抽取100台进行质量调查,在这个问题中表示正确的应该是( )
| A、20000台电视机是总体 |
| B、抽取的100台电视机是总体的一个样本 |
| C、2万台电视机的质量是总体 |
| D、每台电视机是个体 |

 十一国庆节期间,吴家山某眼镜店开展优惠学生配镜的活动,某款式眼镜的广告如图,请你为广告牌补上原价.
十一国庆节期间,吴家山某眼镜店开展优惠学生配镜的活动,某款式眼镜的广告如图,请你为广告牌补上原价. 如图,在梯形ABCD中,AB=4cm,CD=16cm,BC=6
如图,在梯形ABCD中,AB=4cm,CD=16cm,BC=6 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周).
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周). 在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O重合,AC=2,求⊙O的半径r.
在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O重合,AC=2,求⊙O的半径r.