题目内容
7. 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M、N分别为AC、CD的中点,连接BM、MN、BN.求证:BM=MN.
如图,在四边形ABCD中,∠ABC=90°,AC=AD,M、N分别为AC、CD的中点,连接BM、MN、BN.求证:BM=MN.
分析 根据三角形中位线定理得MN=$\frac{1}{2}$AD,根据直角三角形斜边中线定理得BM=$\frac{1}{2}$AC,即可得出结论.
解答 证明:在△CAD中,∵M、N分别是AC、CD的中点,
∴MN∥AD,MN=$\frac{1}{2}$AD,
在Rt△ABC中,∵M是AC中点,
∴BM=$\frac{1}{2}$AC,
∵AC=AD,
∴BM=MN.
点评 本题考查三角形中位线定理、直角三角形斜边中线定理、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
17.下列方程中,解为x=-2的方程是( )
| A. | 2x+5=1-x | B. | 3-2(x-1)=7-x | C. | x-2=-2-x | D. | 1-$\frac{1}{4}$x=$\frac{1}{4}$x |
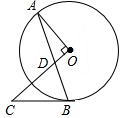 已知,如图,CB是⊙O的切线,切点为B,连接OC,半径OA⊥OC,连接AB交OC于点D,若OD=1,OA=3,则BC=4.
已知,如图,CB是⊙O的切线,切点为B,连接OC,半径OA⊥OC,连接AB交OC于点D,若OD=1,OA=3,则BC=4.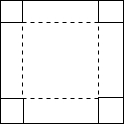 如图,在边长为acm的正方形纸片的四角处各剪去边长为xcm的正方形,然后沿虚线折叠成一个无盖的长方体盒子,则盒子的容积为a2x-4ax2+4x3cm3,当a=8cm,x=1.5cm时,盒子的容积为37.5cm3.
如图,在边长为acm的正方形纸片的四角处各剪去边长为xcm的正方形,然后沿虚线折叠成一个无盖的长方体盒子,则盒子的容积为a2x-4ax2+4x3cm3,当a=8cm,x=1.5cm时,盒子的容积为37.5cm3.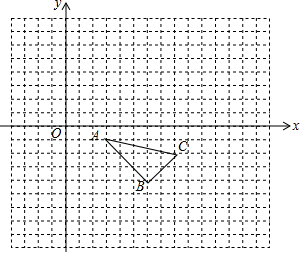 如图,在平面直角坐标系中,△ABC的顶点坐标分别为(3,-1),(6,-4),(8,-2).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为(3,-1),(6,-4),(8,-2).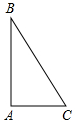 已知:如图在Rt△ABC中,∠BAC=90°.
已知:如图在Rt△ABC中,∠BAC=90°. 已知:如图,△ABC为等边三角形,过AB边上的点D作DG∥BC,交AC于G,在GD的延长线上取点E,使DE=DB,连接AE,CD.
已知:如图,△ABC为等边三角形,过AB边上的点D作DG∥BC,交AC于G,在GD的延长线上取点E,使DE=DB,连接AE,CD.