题目内容
19.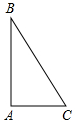 已知:如图在Rt△ABC中,∠BAC=90°.
已知:如图在Rt△ABC中,∠BAC=90°.(1)按要求作出图形:①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE.
(2)猜想(1)中线段 AD与BE的大小关系,并写出证明思路.
分析 (1)根据题意画出图形;
(2)在AE上截取AF=AC,连结BF,证明△ABF≌△ABC,得到BF=BC,∠AFB=∠ACB,证明△ACD≌△EFB,根据全等三角形的性质证明即可.
解答 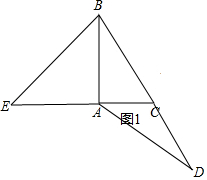 解:(1)完成作图,如图1所示:
解:(1)完成作图,如图1所示:
(2)如图2,在AE上截取AF=AC,连结BF,
在△ABF和△ABC中,
$\left\{\begin{array}{l}{AF=AC}\\{∠FAB=∠CAB}\\{BA=BA}\end{array}\right.$,
∴△ABF≌△ABC(SAS),
∴BF=BC,∠AFB=∠ACB,
∴BF=CD,∠EFB=∠ACD,
在△ACD和△EFB中,
$\left\{\begin{array}{l}{BF=CD}\\{∠BFE=∠ACD}\\{EF=AC}\end{array}\right.$,
∴△ACD≌△EFB(SAS),
∴AD=EB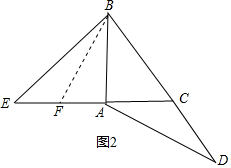 .
.
点评 本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
10.单项式-ab2的系数及次数分别是( )
| A. | 0,3 | B. | -1,3 | C. | 1,3 | D. | -1,2 |
11.如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):

(1)填写如表:
(2)如果原正方形被分割成2016个三角形,此时正方形ABCD内部有多少个点?
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可)

(1)填写如表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | 8 | 10 | … | 2(n+1) |
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可)
9.若a>b,则下列各式中一定成立的是( )
| A. | ma>mb | B. | a2>b2 | C. | 1-a>1-b | D. | b-a<0 |
 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M、N分别为AC、CD的中点,连接BM、MN、BN.求证:BM=MN.
如图,在四边形ABCD中,∠ABC=90°,AC=AD,M、N分别为AC、CD的中点,连接BM、MN、BN.求证:BM=MN. 如图,两车从路段AB的两端同时出发,沿平行路线以相同的速度行驶,相同时间后分别到达C,D两地,CE⊥AB,DF⊥AB,C,D两地到路段AB的距离相等吗?为什么?
如图,两车从路段AB的两端同时出发,沿平行路线以相同的速度行驶,相同时间后分别到达C,D两地,CE⊥AB,DF⊥AB,C,D两地到路段AB的距离相等吗?为什么?