题目内容
2.给出三个多项式:$\frac{1}{2}$x2+2x-1,$\frac{1}{2}$x2+4x+1,$\frac{1}{2}$x2-2x,请选择你最喜欢的两个多项式进行加法运算,并求当x=-2时该式的结果.分析 先根据题意列出式子,再合并同类项化为最简形式,然后将x=-2代入计算即可.
解答 解:情况一:$\frac{1}{2}$x2+2x-1+$\frac{1}{2}$x2+4x+1=x2+6x,当x=-2时,原式=(-2)2+6×(-2)=4-12=-8;
情况二:$\frac{1}{2}$x2+2x-1+$\frac{1}{2}$x2-2x=x2-1,当x=-2时,原式=(-2)2-1=4-1=3;
情况三:$\frac{1}{2}$x2+4x+1+$\frac{1}{2}$x2-2x=x2+2x+1,当x=-2时,原式=(-2)2+2×(-2)+1=4-4+1=1.
点评 此题考查了整式的加减,代数式求值,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握法则是解本题的关键.

练习册系列答案
相关题目
10.单项式-ab2的系数及次数分别是( )
| A. | 0,3 | B. | -1,3 | C. | 1,3 | D. | -1,2 |
11.如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):

(1)填写如表:
(2)如果原正方形被分割成2016个三角形,此时正方形ABCD内部有多少个点?
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可)

(1)填写如表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | 8 | 10 | … | 2(n+1) |
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可)
12.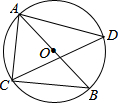 如图,AB是⊙O的直径,C,D是圆上两点,连接AC,BC,AD,CD.若∠CAB=55°,则∠ADB的度数为( )
如图,AB是⊙O的直径,C,D是圆上两点,连接AC,BC,AD,CD.若∠CAB=55°,则∠ADB的度数为( )
 如图,AB是⊙O的直径,C,D是圆上两点,连接AC,BC,AD,CD.若∠CAB=55°,则∠ADB的度数为( )
如图,AB是⊙O的直径,C,D是圆上两点,连接AC,BC,AD,CD.若∠CAB=55°,则∠ADB的度数为( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M、N分别为AC、CD的中点,连接BM、MN、BN.求证:BM=MN.
如图,在四边形ABCD中,∠ABC=90°,AC=AD,M、N分别为AC、CD的中点,连接BM、MN、BN.求证:BM=MN.