题目内容
16. 已知:如图,△ABC为等边三角形,过AB边上的点D作DG∥BC,交AC于G,在GD的延长线上取点E,使DE=DB,连接AE,CD.
已知:如图,△ABC为等边三角形,过AB边上的点D作DG∥BC,交AC于G,在GD的延长线上取点E,使DE=DB,连接AE,CD.(1)求证:△AGE≌△DAC;
(2)把线段DC沿DE方向向左平移,当D平移至点E的位置时,点C恰好与线段BC上的点F重合(如图),请连接AF,并判断△AEF是怎样的三角形,试证明你的结论.
分析 (1)根据已知等边三角形的性质可推出△ADG是等边三角形,从而再利用SAS判定△AGE≌△DAC;
(2)连接AF,由已知可得四边形EFCD是平行四边形,从而得到EF=CD,∠DEF=∠DCF,由(1)知△AGE≌△DAC得到AE=CD,∠AED=∠ACD,从而可得到EF=AE,∠AEF=60°,所以△AEF为等边三角形.
解答 (1)证明:∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ABC=∠ACB=60°.
∵EG∥BC,
∴∠ADG=∠ABC=60°∠AGD=∠ACB=60°.
∴△ADG是等边三角形.
∴AD=DG=AG.
∵DE=DB,
∴EG=AB.
∴GE=AC.
∵EG=AB=CA,
∴∠AGE=∠DAC=60°,
在△AGE和△DAC中,
$\left\{\begin{array}{l}{AG=AD}\\{∠AGE=∠DAC}\\{GE=AC}\end{array}\right.$,
∴△AGE≌△DAC(SAS).
(2)解:△AEF为等边三角形.
证明:如图,连接AF,
∵DG∥BC,EF∥DC,
∴四边形EFCD是平行四边形,
∴EF=CD,∠DEF=∠DCF,
由(1)知△AGE≌△DAC,
∴AE=CD,∠AED=∠ACD.
∵EF=CD=AE,∠AED+∠DEF=∠ACD+∠DCB=60°,
∴△AEF为等边三角形.
点评 此题主要考查学生对全等三角形的判定,等边三角形的性质及判定的理解及运用.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
11.如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):

(1)填写如表:
(2)如果原正方形被分割成2016个三角形,此时正方形ABCD内部有多少个点?
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可)

(1)填写如表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | 8 | 10 | … | 2(n+1) |
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可)
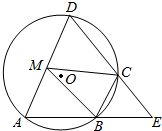 如图所示,四边形ABCD是圆O的内接四边形,AB的延长线与DC的延长线交于点E,且∠D=∠E.
如图所示,四边形ABCD是圆O的内接四边形,AB的延长线与DC的延长线交于点E,且∠D=∠E. 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M、N分别为AC、CD的中点,连接BM、MN、BN.求证:BM=MN.
如图,在四边形ABCD中,∠ABC=90°,AC=AD,M、N分别为AC、CD的中点,连接BM、MN、BN.求证:BM=MN. 如图,两车从路段AB的两端同时出发,沿平行路线以相同的速度行驶,相同时间后分别到达C,D两地,CE⊥AB,DF⊥AB,C,D两地到路段AB的距离相等吗?为什么?
如图,两车从路段AB的两端同时出发,沿平行路线以相同的速度行驶,相同时间后分别到达C,D两地,CE⊥AB,DF⊥AB,C,D两地到路段AB的距离相等吗?为什么? 在边长相同的小正方形组成的网格中,点A、B、C、D都在这些在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则点Bn的坐标是(2n-1,2n-1)(n为正整数).
在边长相同的小正方形组成的网格中,点A、B、C、D都在这些在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则点Bn的坐标是(2n-1,2n-1)(n为正整数).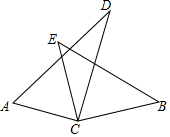 填空,完成下列说理过程
填空,完成下列说理过程