题目内容
16.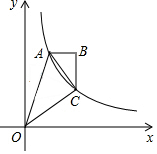 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,AC平分∠OAB,OC平分OA与x轴正半轴的夹角,AB∥x轴,则△OAC的面积是( )
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,AC平分∠OAB,OC平分OA与x轴正半轴的夹角,AB∥x轴,则△OAC的面积是( )| A. | 1.5 | B. | 1.6 | C. | 1.8 | D. | 2 |
分析 延长BC,交x轴于点D,作CE⊥OA于E,设点C(x,y),AB=a,由角平分线的性质得,CD=CE=BC,则△OCD≌△OCE,△COD≌△COE,根据反比例函数的性质,可得出S△OCD=$\frac{1}{2}$xy=1,则S△OCE=$\frac{1}{2}$xy=1,由AB∥x轴,得点A(x-a,2y),由题意得2y(x-a)=2,从而得出三角形ABC的面积等于$\frac{1}{2}$ay,即可得出答案.
解答 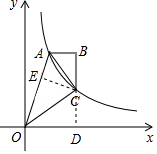 解:延长BC,交x轴于点D,作CE⊥OA于E,
解:延长BC,交x轴于点D,作CE⊥OA于E,
∵∠ABC=90°,AB∥x轴,
∴BD⊥x轴,
设点C(x,y),AB=a,
∵OC平分OA与x轴正半轴的夹角,
∴CD=CE,
∵AC平分∠OAB,
∴BC=CE,
∴AB=BC=CD,
∴点A(x-a,2y),△ABC≌△AEC,△COD≌△COE,
∵双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,
∴S△OCD=$\frac{1}{2}$×2=1,xy=2y(x-a)=2,
∴xy-ay=1,
∵xy=2
∴ay=1,
∴S△ABC=$\frac{1}{2}$ay=$\frac{1}{2}$,
∴SOAC=S△ACE+S△COE=S△ABC+S△COD=1+$\frac{1}{2}$=$\frac{3}{2}$.
故选A.
点评 本题是一道反比例函数的综合题,考查了翻折的性质、反比例函数的性质以及角平分线的性质,难度偏大.

练习册系列答案
相关题目
18.计算-12的相反数是( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
19.若一个正多边形的一个内角是140°,则这个多边形是( )
| A. | 正七边形 | B. | 正八边形 | C. | 正九边形 | D. | 正十边形 |
6. 如图,AB,CD是⊙O的两条弦,连接AD,BC,若∠BCD=50°,则∠BAD的度数为( )
如图,AB,CD是⊙O的两条弦,连接AD,BC,若∠BCD=50°,则∠BAD的度数为( )
 如图,AB,CD是⊙O的两条弦,连接AD,BC,若∠BCD=50°,则∠BAD的度数为( )
如图,AB,CD是⊙O的两条弦,连接AD,BC,若∠BCD=50°,则∠BAD的度数为( )| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
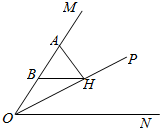 如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.
如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.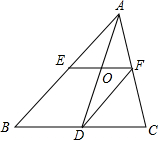 如图,D,E,F分别是△ABC各边的中点.
如图,D,E,F分别是△ABC各边的中点.