题目内容
8.先化简,再求值:$\frac{x-2}{{x}^{2}-1}$÷(1-$\frac{3}{x+1}$),其中x=$\sqrt{3}$+1.分析 被除数的分母利用平方差公式进行因式分解、括号内通过通分进行计算,然后化除法为乘法进行计算.
解答 解:原式=$\frac{x-2}{(x+1)(x-1)}$÷$\frac{x-2}{x+1}$
=$\frac{x-2}{(x+1)(x-1)}$×$\frac{x+1}{x-2}$
=$\frac{1}{x-1}$.
把x=$\sqrt{3}$+1代入,得
原式=$\frac{1}{\sqrt{3}+1-1}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了分式的化简求值和二次根式的化简,是一道常见题.

练习册系列答案
相关题目
10.下列运算正确的是( )
| A. | a2+a2=a4 | B. | (ab)2=ab2 | C. | a6÷a2=a3 | D. | (2a2)3=8a6 |
16.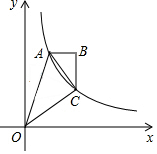 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,AC平分∠OAB,OC平分OA与x轴正半轴的夹角,AB∥x轴,则△OAC的面积是( )
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,AC平分∠OAB,OC平分OA与x轴正半轴的夹角,AB∥x轴,则△OAC的面积是( )
 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,AC平分∠OAB,OC平分OA与x轴正半轴的夹角,AB∥x轴,则△OAC的面积是( )
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,AC平分∠OAB,OC平分OA与x轴正半轴的夹角,AB∥x轴,则△OAC的面积是( )| A. | 1.5 | B. | 1.6 | C. | 1.8 | D. | 2 |
17. 雷达二维平面定位的主要原理是:测量目标的两个信息--距离和角度,目标的表示方法为(γ,α),其中,γ表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为A(5,30°),目标B的位置表示为F(4,150°).用这种方法表示目标C的位置,正确的是( )
雷达二维平面定位的主要原理是:测量目标的两个信息--距离和角度,目标的表示方法为(γ,α),其中,γ表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为A(5,30°),目标B的位置表示为F(4,150°).用这种方法表示目标C的位置,正确的是( )
 雷达二维平面定位的主要原理是:测量目标的两个信息--距离和角度,目标的表示方法为(γ,α),其中,γ表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为A(5,30°),目标B的位置表示为F(4,150°).用这种方法表示目标C的位置,正确的是( )
雷达二维平面定位的主要原理是:测量目标的两个信息--距离和角度,目标的表示方法为(γ,α),其中,γ表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为A(5,30°),目标B的位置表示为F(4,150°).用这种方法表示目标C的位置,正确的是( )| A. | (-3,300°) | B. | (3,60°) | C. | (3,300°) | D. | (-3,60°) |
18.将直线y=2x+3向下平移4个单位长度,得到的直线的函数表达式是( )
| A. | y=2x-1 | B. | y=2x+1 | C. | y=-4x+3 | D. | y=2x+7 |

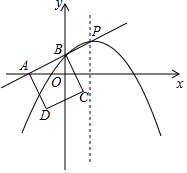 如图,在平面直角坐标系中,直线y=kx+b分别与x轴、y轴交于A、B两点,过点B的抛物线y=-$\frac{1}{4}$(x-2)2+m的顶点P在这条直线上,以AB为边向下方做正方形ABCD.
如图,在平面直角坐标系中,直线y=kx+b分别与x轴、y轴交于A、B两点,过点B的抛物线y=-$\frac{1}{4}$(x-2)2+m的顶点P在这条直线上,以AB为边向下方做正方形ABCD.