题目内容
1．
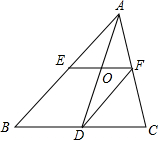如图，D，E，F分别是△ABC各边的中点．（1）若EF=4cm，则BC=8cm，若AB=10m，则DF=5cm
（2）中线AD与中位线EF有什么待殊的关系？试说明理由．
分析 （1）根据三角形中位线定理计算即可；
（2）根据平行四边形的判定和性质解答．
解答 解：（1）∵E，F分别是AB、AC边的中点，
∴BC=2EF=8cm，
同理，DF=$\frac{1}{2}$AB=5cm，
故答案为：8；5；
（2）中线AD与中位线EF互相平分．
连接DE，
根据三角形中位线定理可知，DF=$\frac{1}{2}$AB，DF∥AB，
∵AE=$\frac{1}{2}$AB，
∴AE=DF，
∴四边形AEDF是平行四边形，
∴中线AD与中位线EF互相平分．
点评 本题考查的是三角形中位线定理的应用，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．
练习册系列答案
相关题目
在正方形网格中，网格线的交点称为格点．如图是3×3的正方形网格，已知A，B是两格点，在网格中找一点C，使得△ABC为等腰直角三角形，则这样的点C有（ ）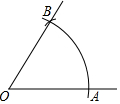
如图，以O为圆心，任意长为半径画弧，与射线OM交于点A，再以A为圆心，AO长为半径画弧，两弧交于点B，画射线OB，则可判定△AOB为等边三角形的依据是三边相等的三角形为等边三角形．
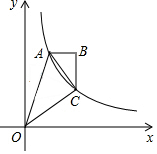如图，双曲线y=$\frac{2}{x}$（x＞0）经过四边形OABC的顶点A、C，∠ABC=90°，AC平分∠OAB，OC平分OA与x轴正半轴的夹角，AB∥x轴，则△OAC的面积是（ ）
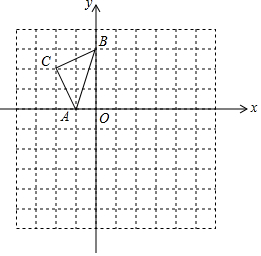如图，在已知的平面直角坐标系中，△ABC的顶点都在正方形网格的格点上，若A，B两点的坐标分别是A（-1，0），B（0，3）．