题目内容
3.已知$\sqrt{a-1}$+(ab-2)2=0,求$\frac{1}{ab}+\frac{1}{(a+1)(b+1)}+\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2015)(b+2015)}$的值.分析 根据$\sqrt{a-1}$+(ab-2)2=0,可以求得a、b的值,从而可以求得$\frac{1}{ab}+\frac{1}{(a+1)(b+1)}+\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2015)(b+2015)}$的值.
解答 解:∵$\sqrt{a-1}$+(ab-2)2=0,
∴$\left\{\begin{array}{l}{a-1=0}\\{ab-2=0}\end{array}\right.$
解得,$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$
∴$\frac{1}{ab}+\frac{1}{(a+1)(b+1)}+\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2015)(b+2015)}$
=$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{2016×2017}$
=$1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{2016}-\frac{1}{2017}$
=1-$\frac{1}{2017}$
=$\frac{2016}{2017}$.
点评 本题考查分式的化简求值、非负数的性质:偶次方、算术平方根,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.圆心角为240°的扇形的半径为3cm,则这个扇形的面积是( )
| A. | πcm2 | B. | 3πcm2 | C. | 9πcm2 | D. | 6πcm2 |
1.已知点A(2-a,a+1)在第二象限,则a的取值范围是( )
| A. | a>2 | B. | -1<a<2 | C. | a<-1 | D. | a<1 |
15.如图1,是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°.折线NG-GH-HE-EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH.如图2,若点H在线段OB时,则$\frac{BH}{OH}$的值是( )
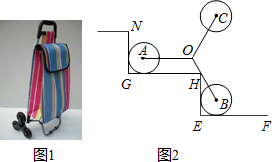

| A. | $\frac{1}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
 如图,点B、C在直线AD上,∠ABE=70°,BF平分∠DBE,CG∥BF,求∠DCG的度数.
如图,点B、C在直线AD上,∠ABE=70°,BF平分∠DBE,CG∥BF,求∠DCG的度数. 如图,矩形OABC的边OA在x轴上,双曲线y=$\frac{k}{x}$与BC交于点D,与AB交于点E,DE=$\frac{1}{2}$OB,矩形OABC的面积为4,则k的值为2.
如图,矩形OABC的边OA在x轴上,双曲线y=$\frac{k}{x}$与BC交于点D,与AB交于点E,DE=$\frac{1}{2}$OB,矩形OABC的面积为4,则k的值为2. 在平面直角坐标系中,反比例函数y=$\frac{k}{x}$的图象过点A($\frac{3}{2}$,2).
在平面直角坐标系中,反比例函数y=$\frac{k}{x}$的图象过点A($\frac{3}{2}$,2).