题目内容
18.等腰三角形三边长分别为a、b、4,且a、b是关于x的一元二次方程x2-12x+k+2=0的两根,则k的值为( )| A. | 30 | B. | 34或30 | C. | 36或30 | D. | 34 |
分析 由等腰三角形的性质可知“a=b,或a、b中有一个数为4”,当a=b时,由根的判别式b2-4ac=0即可得出关于k的一元一次方程,解方程可求出此时k的值;a、b中有一个数为4时,将x=4代入到原方程可得出关于k的一元一次方程,解方程即可求出此时的k值,将k值代入原方程得出a、b的值,结合三角形的三边关系即可得出k=30不合适,综上即可得出结论.
解答 解:∵等腰三角形三边长分别为a、b、4,
∴a=b,或a、b中有一个数为4.
当a=b时,有b2-4ac=(-12)2-4(k+2)=0,
解得:k=34;
当a、b中有一个数为4时,有42-12×4+k+2,
解得:k=30,
当k=30时,原方程为x2-12x+32=0,
解得:x1=4,x2=8,
∵4+4=8,
∴k=30不合适.
故选D.
点评 本题考查了根的判别式、解一元一次方程以及三角形三边关系,解题的关键是分两种情况考虑k值.本题属于基础题,难度不大,解决该题型题目时,根据根的个数结合根的判别式得出关于未知数k的方程(或不等式)是关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
9.若直角三角形的两边长分别为a,b,且满足$\sqrt{{a}^{2}-6a+9}$+|b-4|=0,则该直角三角形的第三边长为( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 4 | D. | 5或$\sqrt{7}$ |
3. 如图为某物体简化的主视图和俯视图,猜想该物体可能是( )
如图为某物体简化的主视图和俯视图,猜想该物体可能是( )
 如图为某物体简化的主视图和俯视图,猜想该物体可能是( )
如图为某物体简化的主视图和俯视图,猜想该物体可能是( )| A. | 光盘 | B. | 双层蛋糕 | C. | 游泳圈 | D. | 铅笔 |
7.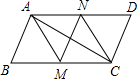 如图,在?ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )
如图,在?ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )
 如图,在?ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )
如图,在?ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )| A. | AM=AN | B. | MN⊥AC | ||
| C. | MN是∠AMC的平分线 | D. | ∠BAD=120° |
 某景区的三个景点A,B,C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.
某景区的三个景点A,B,C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示. 在平面直角坐标系中,反比例函数y=$\frac{k}{x}$的图象过点A($\frac{3}{2}$,2).
在平面直角坐标系中,反比例函数y=$\frac{k}{x}$的图象过点A($\frac{3}{2}$,2).