题目内容
12．A、B两动点分别在数轴-6、12两位置同时向数轴负方向运动，它们的速度分别是2单位长度/秒、4单位长度/秒，另一动点C也在数轴12的位置向数轴负方向运动，当遇到A后，立即返回向B点运动，遇到B点后又立即返回向A点运动，如此往返，直到B追上A时，C立即停止运动．若点C一直以8单位长度/秒的速度匀速运动，那么点C从开始运动到停止运动，行驶的路程是72个单位长度．分析 设B追上A的时间是m秒，由追击问题的数量关系建立方程求出其解，再根据路程=速度×时间就可以得出结论．
解答 解：设B追上A的时间是m秒，由题意，得
4m=2m+18，
解得：m=9
∴点C运动的路程是：8×9=72个单位长度，
故答案为：72
点评 本题考查了行程问题的数量关系的运用，追击问题的等量关系的运用，解答时根据路程=速度×时间建立方程是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
2．
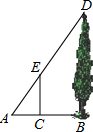已知如图，某学生想利用标杆测量一棵大树的高度，如果标杆EC的高为 1.6m，并测得BC=2.2m，CA=0.8m，那么树DB的高度是（ ）
已知如图，某学生想利用标杆测量一棵大树的高度，如果标杆EC的高为 1.6m，并测得BC=2.2m，CA=0.8m，那么树DB的高度是（ ）| A． | 6m | B． | 5.6m | C． | 5.4m | D． | 4.4m |
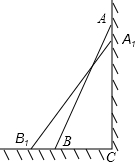如图，一架2.5米长的梯子AB，斜靠在一竖直的墙AC上，这时梯子的顶端A到墙底端C的距离为2.4米，如果梯子的底端B沿CB向外平移0.8米至B1，求梯子顶端A沿墙下滑的距离AA1的长度．
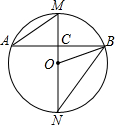如图，MN是⊙O的直径，AB是⊙O的一条弦，且AB⊥MN于点C．
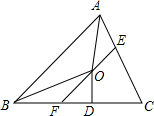如图，在△ABC中，∠BAC和∠ABC的平分线相交于点O，过点O作EF∥AB交BC于F，交AC于E，过点O作OD⊥BC于D，下列四个结论：