题目内容
1.不改变分式的值,使下列分式的分子与分母中的最高次项的系数是正数:(1)$\frac{1-a-{a}^{2}}{1+{a}^{2}-{a}^{3}}$;
(2)$\frac{x+1}{1-{x}^{2}}$;
(3)-$\frac{1-{a}^{3}}{{a}^{2}-a+1}$.
分析 首先将分子、分母均按同一字母的降幂排列,若第一项的系数为负,则添带负号的括号.本题特别注意分子、分母和分式本身的符号的改变.
解答 解:(1)原式=$\frac{-{a}^{2}-a+1}{-{a}^{3}+{a}^{2}+1}$=$\frac{{a}^{2}+a-1}{{a}^{3}-{a}^{2}-1}$;
(2)原式=$\frac{x+1}{-{x}^{2}+1}$=-$\frac{x+1}{{x}^{2}-1}$;
(3)原式=-$\frac{-{a}^{3}+1}{{a}^{2}-a+1}$=$\frac{{a}^{3}-1}{{a}^{2}-a+1}$.
点评 本题考查了分式基本性质,解题的关键是正确运用分式的基本性质.(1)同类分式中的操作可总结成口诀:“一排二添三变”,“一排”即按同一个字母的降幂排列;“二添”是把第一项系数为负号的分子或分母添上带负号的括号;“三变”是按分式变号法则把分子与分母的负号提到分式本身的前边.分式的分子、分母及本身的符号,任意改变其中的两个,分式的值不变.

练习册系列答案
相关题目
11.抛物线y=-x2+3的对称轴是( )
| A. | 直线x=-2 | B. | 直线x=0 | C. | 直线x=-3 | D. | 直线x=3 |
13.在二元一次方程12x+y=8中,当y<0时,x的取值范围是( )
| A. | x<$\frac{2}{3}$ | B. | x>-$\frac{2}{3}$ | C. | x>$\frac{2}{3}$ | D. | x<-$\frac{2}{3}$ |
10.在一个三角形中,最大的内角应满足的条件是( )
| A. | 可以小于60° | B. | 不能小于60° | C. | 可以小于45° | D. | 不能小于120° |
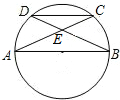 如图,AB是圆O的直径,弦AC,BD相交于点E,若∠BEC=58°,且点C是弧BD的中点,则∠ACD=26°.
如图,AB是圆O的直径,弦AC,BD相交于点E,若∠BEC=58°,且点C是弧BD的中点,则∠ACD=26°.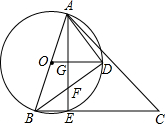 如图,以锐角△ABC的最短边AB的中点O为圆心,AB长为直径作⊙O,交BC于E,连接AE,半径OD⊥弦AE于G,连接AD,BD.
如图,以锐角△ABC的最短边AB的中点O为圆心,AB长为直径作⊙O,交BC于E,连接AE,半径OD⊥弦AE于G,连接AD,BD.