题目内容
17.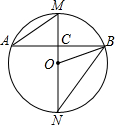 如图,MN是⊙O的直径,AB是⊙O的一条弦,且AB⊥MN于点C.
如图,MN是⊙O的直径,AB是⊙O的一条弦,且AB⊥MN于点C.(1)求证:∠OBN=∠A;
(2)若AB=4$\sqrt{3}$,MC=2,求⊙O的半径.
分析 (1)根据等腰三角形的性质得到∠OBN=∠N,由于∠N=∠A,等量代换得到∠OBN=∠A;
(2)由MN是⊙O的直径,且AB⊥MN于点C,于是得到BC=$\frac{1}{2}$AB=$\frac{1}{2}$×4$\sqrt{3}$=2$\sqrt{3}$,设⊙O的半径为r,根据勾股定理列方程即可得到结论.
解答 解:(1)证明:∵ON=OB,
∴∠OBN=∠N,
∵∠N=∠A,
∴∠OBN=∠A;
(2)解:∵MN是⊙O的直径,且AB⊥MN于点C,
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}$×4$\sqrt{3}$=2$\sqrt{3}$,
设⊙O的半径为r,则OB=OM=r,OC=OM-MC=r-2,
∵OB2=CB2+OC2,
∴r2=(2$\sqrt{3}$)2+(r-2)2,
∴r=4,
∴⊙O的半径=4.
点评 本题考查了垂径定理,勾股定理,圆周角定理,熟练掌握垂径定理是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,已知∠ABC=90°,AC=3,BC=4,以点B为中心将△ABC顺时针旋转,使点落在CB延长线上的点A1处,此时,点C落在点C1的位置,联结AA1、CC1交于点O,CC1与AB交于点D,AA1与BC1交于点E,求四边形BDOE的面积.
如图,在△ABC中,已知∠ABC=90°,AC=3,BC=4,以点B为中心将△ABC顺时针旋转,使点落在CB延长线上的点A1处,此时,点C落在点C1的位置,联结AA1、CC1交于点O,CC1与AB交于点D,AA1与BC1交于点E,求四边形BDOE的面积.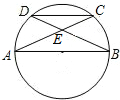 如图,AB是圆O的直径,弦AC,BD相交于点E,若∠BEC=58°,且点C是弧BD的中点,则∠ACD=26°.
如图,AB是圆O的直径,弦AC,BD相交于点E,若∠BEC=58°,且点C是弧BD的中点,则∠ACD=26°.