题目内容
20.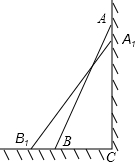 如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯子的顶端A到墙底端C的距离为2.4米,如果梯子的底端B沿CB向外平移0.8米至B1,求梯子顶端A沿墙下滑的距离AA1的长度.
如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯子的顶端A到墙底端C的距离为2.4米,如果梯子的底端B沿CB向外平移0.8米至B1,求梯子顶端A沿墙下滑的距离AA1的长度.
分析 在直角三角形ABC中,已知AB,AC,根据勾股定理即可求BC的长度,根据B1C=B1B+BC即可求得B1C的长度,在直角三角形A1B1C中,已知A1B1=AB,B1C,即可求得A1C的长度,根据AA1=AC-A1C即可求得A1A的长度.
解答  解:根据题意,在Rt△ABC中,AB=2.5,AC=2.4,
解:根据题意,在Rt△ABC中,AB=2.5,AC=2.4,
由勾股定理得:
BC=$\sqrt{2.{5}^{2}-2.{4}^{2}}$=0.7,
∵BB1=0.8,
∴B1C=B1B+BC=1.5.
∵在Rt△A1B1C中,A1B1=2.5,B1C=1.5,
∴A1C=$\sqrt{2.{5}^{2}-1.{5}^{2}}$=2,
∴A1A=2.4-2=0.4.
答:那么梯子顶端沿墙下滑的距离为0.4米.
点评 本题考查的是勾股定理的应用及勾股定理在直角三角形中的正确运用,本题中求B1C的长度是解题的关键.

练习册系列答案
相关题目
10.张华记录了今年雨季钱塘江一周内水位变化的情况如下表(正号表示比前一天高,负号表示比前一天低):
(1)本周星期二水位最高,星期日水位最低.
(2)与上周末相比,本周日的水位是上升了还是下降了?(写出计算过程)
(2)请用折线统计图表示钱塘江一周内水位变化的情况.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 水位变化(m) | +0.25 | +0.80 | -0.40 | +0.03 | +0.28 | -0.36 | -0.04 |
(2)与上周末相比,本周日的水位是上升了还是下降了?(写出计算过程)
(2)请用折线统计图表示钱塘江一周内水位变化的情况.
11.抛物线y=-x2+3的对称轴是( )
| A. | 直线x=-2 | B. | 直线x=0 | C. | 直线x=-3 | D. | 直线x=3 |
10.在一个三角形中,最大的内角应满足的条件是( )
| A. | 可以小于60° | B. | 不能小于60° | C. | 可以小于45° | D. | 不能小于120° |
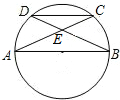 如图,AB是圆O的直径,弦AC,BD相交于点E,若∠BEC=58°,且点C是弧BD的中点,则∠ACD=26°.
如图,AB是圆O的直径,弦AC,BD相交于点E,若∠BEC=58°,且点C是弧BD的中点,则∠ACD=26°.