题目内容
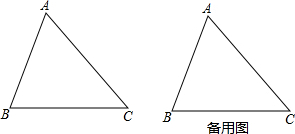 如图,△ABC中,AB=13,BC=14,AC=15.点P从点B出发,以每秒2个单位的速度沿射线BC运动.设点P运动的时间为t秒,求当t为何值时,△ABP为等腰三角形?
如图,△ABC中,AB=13,BC=14,AC=15.点P从点B出发,以每秒2个单位的速度沿射线BC运动.设点P运动的时间为t秒,求当t为何值时,△ABP为等腰三角形?考点:等腰三角形的判定
专题:动点型
分析:作AD⊥BC于D,如图1,设AD=y,BD=x,则CD=BC-BD=14-x,利用勾股定理得到x2+y2=132,(14-x)2+y2=152,消去y可解得x=5,即BD=5,然后分类讨论:当BP=BA时,△ABP为等腰三角形,即2t=13,解得t=
(s);当AP=AB时,△ABP为等腰三角形,如图2,则PB=2BD,即2t=2×5,解得t=5(s);作AB的中垂线交AB于Q,交BC于P,则PA=PB,△ABP为等腰三角形,如图3,证明Rt△BPQ∽Rt△BAD,利用相似比得到
=
,解得t=
(s).
| 13 |
| 2 |
| 2t |
| 13 |
| ||
| 5 |
| 169 |
| 20 |
解答:解:作AD⊥BC于D,如图1,设AD=y,BD=x,则CD=BC-BD=14-x,

在Rt△ABD中,x2+y2=132①,
在Rt△ACD中,(14-x)2+y2=152②,
②-①得142-28x=28×2,解得x=5,
∴BD=5,
当BP=BA时,△ABP为等腰三角形,即2t=13,解得t=
(s);
当AP=AB时,△ABP为等腰三角形,则AD垂值平分BP,如图2,

∴PB=2BD,即2t=2×5,
∴t=5(s);
作AB的中垂线交AB于Q,交BC于P,则PA=PB,△ABP为等腰三角形,
如图3,

则BQ=
AB=
,BP=2t,
∵∠PBQ=∠ABD,
∴Rt△BPQ∽Rt△BAD,
∴
=
,即
=
,
∴t=
(s),
综上所述,当t为
s或5s或
s时,△ABP为等腰三角形.

在Rt△ABD中,x2+y2=132①,
在Rt△ACD中,(14-x)2+y2=152②,
②-①得142-28x=28×2,解得x=5,
∴BD=5,
当BP=BA时,△ABP为等腰三角形,即2t=13,解得t=
| 13 |
| 2 |
当AP=AB时,△ABP为等腰三角形,则AD垂值平分BP,如图2,

∴PB=2BD,即2t=2×5,
∴t=5(s);
作AB的中垂线交AB于Q,交BC于P,则PA=PB,△ABP为等腰三角形,
如图3,

则BQ=
| 1 |
| 2 |
| 13 |
| 2 |
∵∠PBQ=∠ABD,
∴Rt△BPQ∽Rt△BAD,
∴
| PB |
| AB |
| BQ |
| BD |
| 2t |
| 13 |
| ||
| 5 |
∴t=
| 169 |
| 20 |
综上所述,当t为
| 13 |
| 2 |
| 169 |
| 20 |
点评:本题考查了等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等.也考查了勾股定理和分类讨论的思想.

练习册系列答案
相关题目
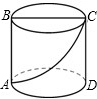 如图所示,是一圆柱体,已知圆柱的高AB=3,底面直径BC=10,现在有一只蚂蚁想要从A处沿圆柱表面爬行到对角C处去捕食,则它爬行最短路径是( )(本题π取3).
如图所示,是一圆柱体,已知圆柱的高AB=3,底面直径BC=10,现在有一只蚂蚁想要从A处沿圆柱表面爬行到对角C处去捕食,则它爬行最短路径是( )(本题π取3).| A、13 | ||
B、3
| ||
C、
| ||
D、2
|
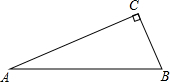 如图,Rt△ABC中,∠C=90°,∠B=α,将△ABC绕点C逆时针旋转得到△A′B′C,当点A′落在直线AB上时,旋转角为β(其中0°<β<180°),那么β与α之间的数量关系为( )
如图,Rt△ABC中,∠C=90°,∠B=α,将△ABC绕点C逆时针旋转得到△A′B′C,当点A′落在直线AB上时,旋转角为β(其中0°<β<180°),那么β与α之间的数量关系为( )| A、β=180°-α | ||
| B、β=90°+α | ||
C、β=
| ||
| D、β=2α |
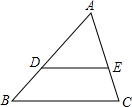 如图,△ABC中,D、E分别为边AB、AC上的点,且DE∥BC,下列判断错误的是( )
如图,△ABC中,D、E分别为边AB、AC上的点,且DE∥BC,下列判断错误的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知A(3,0)、B(0,4),以A为顶点的抛物线与y轴交于点B.
如图,已知A(3,0)、B(0,4),以A为顶点的抛物线与y轴交于点B.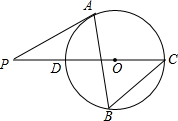 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.